Question

【题目】如图，平行四边形ABCD中，AB=18，BC＝12，∠DAB＝60°，E在AB上，且AE：EB＝1：2，F是BC的中点，过D分别作DP⊥AF于P，DQ⊥CE于Q，则下列结论正确的个数是（　　）

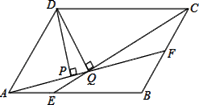
（1）CE平分∠BCD；（2）AF=CE；（3）连接DE、DF，则；（4）DP：DQ=

A.4个B.3个C.2个D.1个

Answer 1

【答案】B

【解析】

由平行四边形ABCD中，AB=18，BC＝12，AE：EB＝1：2，得EB= BC，结合AB∥CD，即可判断（1）；过点F作FM⊥AB交AB的延长线于点M，在RtAMF中，利用勾股定理求出AF=，在BCE中，求出CE的值，即可判断（2）；由，，即可判断（3）；由，即可判断（4）．

∵平行四边形ABCD中，AB=18，BC＝12，AE：EB＝1：2，

∴EB= BC＝12，

∴∠BEC=∠BCE，

∵AB∥CD，

∴∠BEC=∠DCE，

∴∠BCE=∠DCE，

∴CE平分∠BCD，

∴（1）正确；

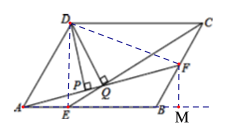
过点F作FM⊥AB交AB的延长线于点M，

∵AD∥BC，

∴∠CBM=∠DAB＝60°，∠BFM=30°，

∵F是BC的中点，

∴BF=BC=6，

∴BM=BF=3，FM=BM=3，

∴AM=18+3=21，

∴AF=，

∵EB= BC＝12，∠ABC=180°-60°=120°，

∴CE=×BC=12，

∴AF≠CE，

∴（2）错误；

∵在平行四边形ABCD中，，，

∴，

∴（3）正确；

∵DP⊥AF，DQ⊥CE，

∴，

∴DP：DQ=CE：AF=，

∴（4）正确．

故答案是：span>B．