题目内容
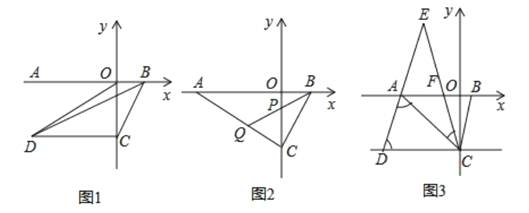
【题目】如图:在平面直角坐标系xOy中,A(4,0)、B(0,3)、C(4,3),I是△ABC的内心,将△ABC绕原点逆时针旋转90°后,I的对应点I′的坐标为( )
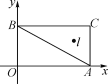
A. (-2,3) B. (-3,2) C. (3,-2) D. (2,-3)
【答案】A
【解析】
直接利用直角三角形的性质得出其内切圆半径,进而得出I点坐标,再利用旋转的性质得出对应点坐标.
过点作IF⊥AC于点F,IE⊥OA于点E,
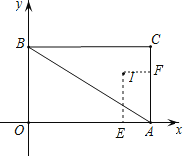
∵A(4,0),B(0,3),C(4,3),
∴BC=4,AC=3,
则AB=5,
∵I是△ABC的内心,
∴I到△ABC各边距离相等,等于其内切圆的半径,
∴IF=1,故I到BC的距离也为1,
则AE=1,
故IE=3﹣1=2,
OE=4﹣1=3,
则I(3,2),
∵△ABC绕原点逆时针旋转90°,
∴I的对应点I'的坐标为:(﹣2,3),
故选A.

练习册系列答案
相关题目