题目内容
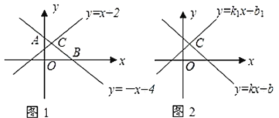
【题目】![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为直线
为直线![]() 上一动点(点
上一动点(点![]() 不与
不与![]() 、
、![]() 重合),以
重合),以![]() 为边在
为边在![]() 右侧作等腰直角三角形
右侧作等腰直角三角形![]() ,使
,使![]() ,连接
,连接![]() .
.
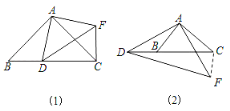
(1)如图1,当点![]() 在线段
在线段![]() 上时;证明
上时;证明
①![]()
②![]()
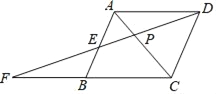
(2)如图2,当点![]() 在线段
在线段![]() 的延长线上时,结论(1)中的①、②是否仍然成立?若成立,请给予证明:若不成立,请你写出正确结论再给予证明.
的延长线上时,结论(1)中的①、②是否仍然成立?若成立,请给予证明:若不成立,请你写出正确结论再给予证明.
【答案】(1)①见解析;②见解析;(2)结论(1)①成立,理由见解析;②不成立,![]() ,理由见解析.
,理由见解析.
【解析】
(1)①根据等腰直角三角形的性质可得![]() ,
,![]() ,
,![]() ,∠B=∠ACB=45°,然后利用SAS即可证出
,∠B=∠ACB=45°,然后利用SAS即可证出![]() ,从而得出
,从而得出![]() ,即可证出结论;
,即可证出结论;
②根据①中全等可得![]() ,从而证出结论;
,从而证出结论;
(2)根据等腰直角三角形的性质可得![]() ,
,![]() ,
,![]() ,然后利用SAS即可证出
,然后利用SAS即可证出![]() ,从而得出
,从而得出![]() ,然后根据三角形外角的性质可得
,然后根据三角形外角的性质可得![]() 即可证出结论;根据
即可证出结论;根据![]() 可得
可得![]() ,从而证出结论.
,从而证出结论.
证明:(1)①![]() 与
与![]() 都是等腰直角三角形,
都是等腰直角三角形,
![]() ,
,![]() ,
,![]() ,∠ABC=∠ACB=45°
,∠ABC=∠ACB=45°
![]() ,
,
在△ADB和△AFC中
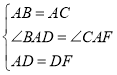
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
②![]() ,
,
![]() ,
,
![]() .
.
(2)解:结论(1)①成立.
理由:![]() 与
与![]() 都是等腰直角三角形,
都是等腰直角三角形,
![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
在△ADB和△AFC中
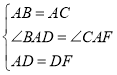
![]() ,
,
![]() ,
,
∵![]() ,
,
![]() ,
,
![]()
![]() .
.
②不成立,正确的结论:![]()
![]() ,
,
![]() ,
,
![]() .
.

练习册系列答案
相关题目
【题目】九年级甲、乙两名同学期末考试的成绩(单位:分)如下:
语文 | 数学 | 英语 | 历史 | 理化 | 体育 | |
甲 | 75 | 93 | 85 | 84 | 95 | 90 |
乙 | 85 | 85 | 91 | 85 | 89 | 85 |
根据表格中的数据,回答下列问题:
(1)甲的总分为522分,则甲的平均成绩是__________分,乙的总分为520分,________的成绩好一些. (填“甲”或者“乙”)
(2)经过计算知![]() . 你认为__________不偏科;(填“甲”或者“乙”)
. 你认为__________不偏科;(填“甲”或者“乙”)
(3)中招录取时,历史和体育科目的权重是0.3,其它科成绩权重是1,请问谁的成绩更好一些?请说明理由.