ЬтФПФкШн
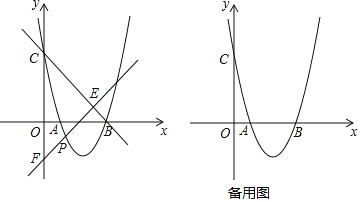
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=x2+bx+cгыxжсНЛгкAЁЂBСНЕуЃЌBЕузјБъЮЊЃЈ4ЃЌ0ЃЉЃЌгыyжсНЛгкЕуCЃЈ0ЃЌ4ЃЉЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
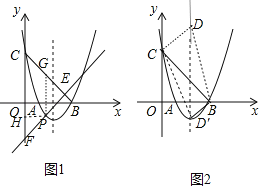
ЃЈ2ЃЉЕуPдкxжсЯТЗНЕФХзЮяЯпЩЯЃЌЙ§ЕуPЕФжБЯпy=x+mгыжБЯпBCНЛгкЕуEЃЌгыyжсНЛгкЕуFЃЌЧѓPE+EFЕФзюДѓжЕЃЛ
ЃЈ3ЃЉЕуDЮЊХзЮяЯпЖдГЦжсЩЯвЛЕуЃЎ
ЂйЕБЁїBCDЪЧвдBCЮЊжБНЧБпЕФжБНЧШ§НЧаЮЪБЃЌжБНгаДГіЕуDЕФзјБъЃЛ
ЂкШєЁїBCDЪЧШёНЧШ§НЧаЮЃЌжБНгаДГіЕуDЕФзнзјБъnЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉХзЮяЯпЕФНтЮіЪНЮЊy=x2Љ5x+4ЃЛЃЈ2ЃЉPE+EFЕФзюДѓжЕЮЊ![]() ЃЛЃЈ3ЃЉЂйЗћКЯЬѕМўЕФЕуDЕФзјБъЪЧЃЈ
ЃЛЃЈ3ЃЉЂйЗћКЯЬѕМўЕФЕуDЕФзјБъЪЧЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЛЂкЕуDЕФзнзјБъЕФШЁжЕЗЖЮЇЮЊ
ЃЉЃЛЂкЕуDЕФзнзјБъЕФШЁжЕЗЖЮЇЮЊ![]() ЃМyЃМ
ЃМyЃМ![]() ЛђЉ
ЛђЉ![]() ЃМyЃМ
ЃМyЃМ![]() ЃЎ
ЃЎ
ЁОНтЮіЁПЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉвзЕУBCЕФНтЮіЪНЮЊy=Љx+4ЃЌЯШжЄУїЁїECFЮЊЕШбќжБНЧШ§НЧаЮЃЌзїPHЁЭyжсгкHЃЌPGЁЮyжсНЛBCгкGЃЌШчЭМ1ЃЌдђЁїEPGЮЊЕШбќжБНЧШ§НЧаЮЃЌPE=![]() PGЃЌЩшPЃЈtЃЌt2Љ4t+3ЃЉЃЈ1ЃМtЃМ3ЃЉЃЌдђGЃЈtЃЌЉt+3ЃЉЃЌНгзХРћгУtБэЪОPFЁЂPEЃЌЫљвдPE+EF=2PE+PF=Љ
PGЃЌЩшPЃЈtЃЌt2Љ4t+3ЃЉЃЈ1ЃМtЃМ3ЃЉЃЌдђGЃЈtЃЌЉt+3ЃЉЃЌНгзХРћгУtБэЪОPFЁЂPEЃЌЫљвдPE+EF=2PE+PF=Љ![]() t2+5
t2+5![]() tЃЌШЛКѓРћгУЖўДЮКЏЪ§ЕФаджЪНтОіЮЪЬтЃЛ
tЃЌШЛКѓРћгУЖўДЮКЏЪ§ЕФаджЪНтОіЮЪЬтЃЛ
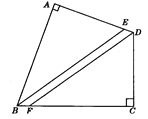
ЃЈ3ЃЉЂйШчЭМ2ЃЌХзЮяЯпЕФЖдГЦжсЮЊжБЯпx=ЉЕуDЕФзнзјБъЕФШЁжЕЗЖЮЇЃЛ
ЂкгЩгкЁїBCDЪЧвдBCЮЊаББпЕФжБНЧШ§НЧаЮга4+ЃЈyЉ3ЃЉ2+1+y2=18ЃЌНтЕУy1=![]() ЃЌy2=
ЃЌy2=![]() ЃЌЕУЕНДЫЪБDЕузјБъЮЊЃЈ
ЃЌЕУЕНДЫЪБDЕузјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌШЛКѓНсКЯЭМаЮПЩШЗЖЈЁїBCDЪЧШёНЧШ§НЧаЮЪБЕуDЕФзнзјБъЕФШЁжЕЗЖЮЇЃЎ
ЃЉЃЌШЛКѓНсКЯЭМаЮПЩШЗЖЈЁїBCDЪЧШёНЧШ§НЧаЮЪБЕуDЕФзнзјБъЕФШЁжЕЗЖЮЇЃЎ
ЃЈ1ЃЉАбBЃЈ4ЃЌ0ЃЉЃЌCЃЈ0ЃЌ4ЃЉДњШыy=x2+bx+cЃЌЕУ
![]() ЃЌ
ЃЌ
НтЕУ ![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊy=x2Љ5x+4ЃЛ
ЃЈ2ЃЉгЩBЃЈ4ЃЌ0ЃЉЃЌCЃЈ0ЃЌ4ЃЉЃЌИљОнД§ЖЈЯЕЪ§ЗЈвзЕУBCЕФНтЮіЪНЮЊy=Љx+4ЃЌ
ЁпжБЯпy=x+mгыжБЯпy=xЦНааЃЌ
ЁржБЯпy=Љx+4гыжБЯпy=x+mДЙжБЃЌ
ЁрЁЯCEF=90ЁуЃЌ
ЁрЁїECFЮЊЕШбќжБНЧШ§НЧаЮЃЌ
зїPHЁЭyжсгкHЃЌPGЁЮyжсНЛBCгкGЃЌШчЭМ1ЃЌЁїEPGЮЊЕШбќжБНЧШ§НЧаЮЃЌPE=![]() PGЃЌ
PGЃЌ
ЩшPЃЈtЃЌt2Љ5t+4ЃЉЃЈ1ЃМtЃМ4ЃЉЃЌдђGЃЈtЃЌЉt+4ЃЉЃЌ
ЁрPF=![]() PH=
PH=![]() tЃЌPG=Љt+4ЉЃЈt2Љ5t+4ЃЉ=Љt2+4tЃЌ
tЃЌPG=Љt+4ЉЃЈt2Љ5t+4ЃЉ=Љt2+4tЃЌ
ЁрPE=![]() PG=Љ
PG=Љ![]() t2+2
t2+2![]() tЃЌ
tЃЌ
ЁрPE+EF=PE+PE+PF=2PE+PF=Љ![]() t2+4
t2+4![]() t+
t+![]() t=Љ
t=Љ![]() t2+5
t2+5![]() t=Љ
t=Љ![]() ЃЈtЉ
ЃЈtЉ![]() ЃЉ2+
ЃЉ2+![]() ЃЌ
ЃЌ
ЕБt=![]() ЪБЃЌPE+EFЕФзюДѓжЕЮЊ
ЪБЃЌPE+EFЕФзюДѓжЕЮЊ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЂйШчЭМ2ЃЌХзЮяЯпЕФЖдГЦжсЮЊжБЯпx=![]() ЃЌ
ЃЌ
ЩшDЃЈ![]() ЃЌyЃЉЃЌдђBC2=42+42=32ЃЌDC2=ЃЈ
ЃЌyЃЉЃЌдђBC2=42+42=32ЃЌDC2=ЃЈ![]() ЃЉ2+ЃЈyЉ4ЃЉ2ЃЌBD2=ЃЈ4Љ
ЃЉ2+ЃЈyЉ4ЃЉ2ЃЌBD2=ЃЈ4Љ![]() ЃЉ2+y2=
ЃЉ2+y2=![]() +y2ЃЌ
+y2ЃЌ
ЕБЁїBCDЪЧвдBCЮЊжБНЧБпЃЌBDЮЊаББпЕФжБНЧШ§НЧаЮЪБЃЌBC2+DC2=BD2ЃЌ
МД32+ЃЈ![]() ЃЉ2+ЃЈyЉ4ЃЉ2=
ЃЉ2+ЃЈyЉ4ЃЉ2=![]() +y2ЃЌНтЕУy=5ЃЌДЫЪБDЕузјБъЮЊЃЈ
+y2ЃЌНтЕУy=5ЃЌДЫЪБDЕузјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЕБЁїBCDЪЧвдBCЮЊжБНЧБпЃЌCDЮЊаББпЕФжБНЧШ§НЧаЮЪБЃЌBC2+DB2=DC2ЃЌ
МД32+![]() +y2=ЃЈ
+y2=ЃЈ![]() ЃЉ2+ЃЈyЉ4ЃЉ2ЃЌНтЕУy=Љ1ЃЌДЫЪБDЕузјБъЮЊЃЈ
ЃЉ2+ЃЈyЉ4ЃЉ2ЃЌНтЕУy=Љ1ЃЌДЫЪБDЕузјБъЮЊЃЈ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЛ
ЃЉЃЛ
злЩЯЫљЪіЃЌЗћКЯЬѕМўЕФЕуDЕФзјБъЪЧЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЛ
ЃЉЃЛ
ЂкЕБЁїBCDЪЧвдBCЮЊаББпЕФжБНЧШ§НЧаЮЪБЃЌDC2+DB2=BC2ЃЌМДЃЈ![]() ЃЉ2+ЃЈyЉ4ЃЉ2+
ЃЉ2+ЃЈyЉ4ЃЉ2+![]() +y2=32ЃЌНтЕУy1=
+y2=32ЃЌНтЕУy1=![]() ЃЌy2=
ЃЌy2=![]() ЃЌДЫЪБDЕузјБъЮЊЃЈ
ЃЌДЫЪБDЕузјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЫљвдЁїBCDЪЧШёНЧШ§НЧаЮЃЌЕуDЕФзнзјБъЕФШЁжЕЗЖЮЇЮЊ![]() ЃМyЃМ
ЃМyЃМ![]() ЛђЉ
ЛђЉ![]() ЃМyЃМ
ЃМyЃМ![]() ЃЎ
ЃЎ