Question

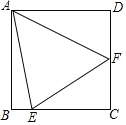
【题目】如图，平行四边形ABCD的对角线AC的垂直平分线与对角线AC交于点O，与边AD、BC分别交于点E、F，那么四边形AFCE是不是菱形？为什么？

Answer 1

【答案】四边形AFCE是菱形，理由详见解析.

【解析】

根据平行四边形ABCD的性质可得AD∥BC；然后由两直线平行，内错角相等，得∠OAE=∠OCF，根据ASA可证明△AOE≌△COF，可得AE=CF，即可证明四边形AFCE是平行四边形，根据垂直平分线的性质可得

四边形AFCE是菱形，理由：

∵四边形ABCD是平行四边形，

∴AD∥BC，即AE∥FC．

∴∠OAE＝∠OCF．

∵∠AOE＝∠COF＝90°，AO＝CO，

∴△AOE≌△COF，

∴AE＝CF，

∴四边形AFCE是平行四边形．

∵EF⊥AC于O，

∴平行四边形AFCE是菱形．