Question

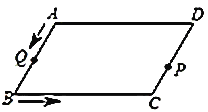
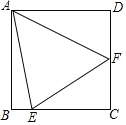
【题目】如图，在正方形ABCD中，AB＝BC＝CD＝DA，∠BAD＝∠ABC＝∠BCD＝∠ADC＝90°，E、F为BC、CD边上的点，若∠FAE＝45°，试探究线段BE、EF、DF之间的数量关系，并说明理由．

Answer 1

【答案】EF＝BE+DF，见解析.

【解析】

将△DAF绕点A顺时针旋转90°，得到△BAH，可得∠DAF＝∠BAH，AF＝AH，∠FAH＝90°，由“SAS”可证△FAE≌△HAE，可得EF＝HE＝BE＋DF．

解：EF＝BE+DF．

理由如下：

如图，将△DAF绕点A顺时针旋转90°，得到△BAH，

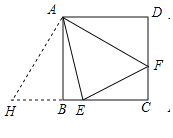
∴△ADF≌△ABH，

∴∠DAF＝∠BAH，AF＝AH，

∴∠FAH＝90°，

∴∠EAF＝∠EAH＝45°，

∵AF＝AH，∠FAE＝∠HAE，AE＝AE

∴△FAE≌△HAE（SAS），

∴EF＝HE

∴EF＝HE＝BE+HB，

∴EF＝BE+DF．