题目内容
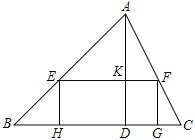
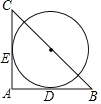
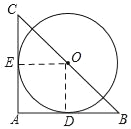
【题目】如图,在Rt△ABC中,∠A=90°,BC=4,以BC的中点O为圆心分别与AB,AC相切于D、E两点,则![]() 的长为( )
的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]() π
π
【答案】C
【解析】
连接OE、OD,由切线的性质可知OE⊥AC,OD⊥AB,由于O是BC的中点,从而可知OD是中位线,所以可知∠B=45°,从而可知半径r的值,最后利用弧长公式即可求出答案.
解:连接OE、OD,
设半径为r,
∵⊙O分别与AB,AC相切于D,E两点,
∴OE⊥AC,OD⊥AB,
∵O是BC的中点,
∴OD是中位线,
∴OD=AE=![]() AC,
AC,
∴AC=2r,
同理可知:AB=2r,
∴AB=AC,
∴∠B=45°,
∵BC=4,
∴由勾股定理可知AB=2![]() ,
,
∴r=![]() ,
,
∴![]() .
.
故选:C.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
【题目】在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
黑棋数 | 2 | 5 | 1 | 5 | 4 | 7 | 4 | 3 | 3 | 6 |
根据以上数据,解答下列问题:
(I)直接填空:第10次摸棋子摸到黑棋子的频率为 ;
(Ⅱ)试估算袋中的白棋子数量.