Question

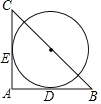
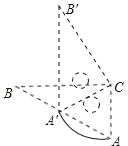
【题目】如图，△ABC和△A'B′C是两个完全重合的直角三角板，∠B＝30°，斜边长为10cm．三角板A′B′C绕直角顶点C顺时针旋转，当点A落在AB边上时．（1）求CA旋转到CA′所构成的扇形的弧长．（2）判断BC与A′B′的位置关系．

Answer 1

【答案】（1）π（cm）；（2）BC⊥A′B′．

【解析】

（1）根据三角形内角和定理和直角三角形的性质得到，∠A＝60°，根据旋转的性质得到CA＝CA′，根据弧长公式计算；

（2）根据旋转变换的性质求出∠BCB′＝60°，根据垂直的定义证明．

解：（1）∵∠ACB＝90°，∠B＝30°，

∴，∠A＝60°，

由题意得，CA＝CA′，

∴△CAA′为等边三角形，

∴∠ACA′＝60°，

∴CA旋转到CA′所构成的扇形的弧长＝（cm）；

（2）BC⊥A′B′，

理由如下：∵∠ACA′＝60°，

∴∠BCA′＝30°，

∴∠BCB′＝60°，又∠B′＝30°，

∴BC⊥A′B′．