题目内容
【题目】如图，长方形ABCD中，AB=4cm，BC=6cm，现有一动点P从A出发以2cm/秒的速度，沿矩形的边A﹣B﹣C运动，设点P运动的时间为t秒．
（1）当t为何值时，点P与点A的距离为5cm？
（2）当t为何值时，△APD是等腰三角形？
（3）当t为何值时，（2＜t＜5），以线段AD、CP、AP的长度为三边长的三角形是直角三角形，且AP是斜边？
【答案】
（1）
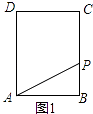
解：如图1，若点P在BC上，
∵在Rt△ABP中，AP=5，AB=4
∴BP=2t﹣4=3，
∴t= 
；
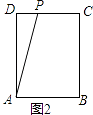
如图2，若点P在DC上，
则在Rt△ADP中，AP是斜边，
∵AD=6，
∴AP＞6，
∴AP≠5．
综上所述，当t= 秒时，点P与点A的距离为5cm
（2）
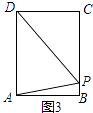
解：）当AD=DP时，如图3，PC=（10﹣2t）cm，CD=4cm，DP=6cm，
∵CD2+PC2=DP2，即42+（10﹣2t）2=62，解得t=5± 
，即t1=5+ ，t2=5﹣ ；
当DP=AP时，如图4，PC=PB=3cm，
∵AB=4cm，
∴AB+BP=4+3=7cm，
∴t= （秒）；
当AD=AP=6时，PB=2t﹣4，
∵AB2+BP2=AP2，即42+（2t﹣4）2=62，解得t=2+ 或t=2﹣ （舍去），
综上所述，当t=（5± ）秒或t= 秒时，△APD是等腰三角形
（3）
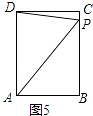
解：当2＜t＜5时，点P在BC边上，
∵BP=2t﹣4，CP=10﹣2t，
∴AP2=AB2+BP2=42+（2t﹣4）2
由题意，有AD2+CP2=AP2
∴62+（10﹣2t）2=42+（2t﹣4）2
∴t= 
＜5，
∴t= ．
答：当t= 秒时，以线段AD、CP、AP的长度为三边长的三角形是直角三角形，且AP是斜边
【解析】（1）分为两种情况：P在BC上，P在DC上，根据勾股定理得出关于t的方程，求出即可；（2）分AD=DP，DP=AP，AD=AP三种情况进行讨论；（3）求出BP=2t﹣4，CP=10﹣2t，根据AP2=AB2+BP2=42+（2t﹣4）2和AD2+CP2=AP2得出方程62+（10﹣2t）2=42+（2t﹣4）2 ， 求出方程的解即可．
【考点精析】利用勾股定理的概念对题目进行判断即可得到答案，需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．
