题目内容
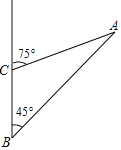
【题目】定义:点P(a,b)关于原点的对称点为P',以PP'为边作等边△PP'C,则称点C为P的“等边对称点”;
(1)若P(1,![]() ),求点P的“等边对称点”的坐标.
),求点P的“等边对称点”的坐标.
(2)若P点是双曲线y=![]() (x>0)上一动点,当点P的“等边对称点”点C在第四象限时,
(x>0)上一动点,当点P的“等边对称点”点C在第四象限时,
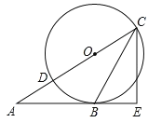
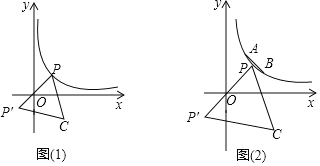
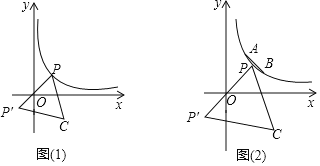
①如图(1),请问点C是否也会在某一函数图象上运动?如果是,请求出此函数的解析式;如果不是,请说明理由.
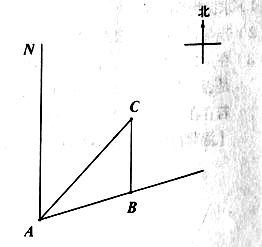
②如图(2),已知点A(1,2),B(2,1),点G是线段AB上的动点,点F在y轴上,若以A、G、F、C这四个点为顶点的四边形是平行四边形时,求点C的纵坐标yc的取值范围.
【答案】(1)(3,![]() );(2)①是,y=﹣
);(2)①是,y=﹣![]() (x>0);②yc≤﹣6或﹣3<yc≤﹣2
(x>0);②yc≤﹣6或﹣3<yc≤﹣2
【解析】
(1)P(1,![]() )则P'(﹣1,﹣
)则P'(﹣1,﹣![]() ),可求PP'=4;设C(m,n),有PC=P'C=4,通过解方程可得m=﹣
),可求PP'=4;设C(m,n),有PC=P'C=4,通过解方程可得m=﹣![]() n,再进行运算即可;
n,再进行运算即可;
(2)①设P(c,![]() )则P'(﹣c,﹣
)则P'(﹣c,﹣![]() ),可求PP'=2
),可求PP'=2![]() ;设C(s,t),有PC=P'C=2
;设C(s,t),有PC=P'C=2![]() ,通过解方程可得s=﹣
,通过解方程可得s=﹣![]() ,t=
,t=![]() c,令
c,令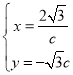 ,消元c即可得xy=﹣6;
,消元c即可得xy=﹣6;
②当AG为平行四边形的边时,G与B重合时,为一临界点通过平移可求得C(1,﹣6),yc≤﹣6;
当AG为平行四边形的对角线时,G与B重合时,求得C(3,﹣2),G与A重合时,C(2,﹣3),此时﹣3<yc≤﹣2.
解:(1)∵P(1,![]() ),
),
∴P'(﹣1,﹣![]() ),
),
∴PP'=4,
设C(m,n),
∴等边△PP′C,
∴PC=P'C=4,
∴![]() ,
,
∴m=﹣![]() n,
n,
∴(﹣![]() n﹣1)2+(n﹣
n﹣1)2+(n﹣![]() )2=16.
)2=16.
解得n=![]() 或﹣
或﹣![]() ,
,
∴m=﹣3或m=3.
如图1,观察点C位于第四象限,则C(﹣3,![]() ).即点P的“等边对称点”的坐标是(3,
).即点P的“等边对称点”的坐标是(3,![]() ).
).
(2)①设P(c,![]() ),
),
∴P'(﹣c,﹣![]() ),
),
∴PP'=2![]() ,
,
设C(s,t),
PC=P'C=2![]() ,
,
∴![]() ,
,
∴s=﹣![]() ,
,
∴t2=3c2,
∴t=![]() c,
c,
∴C(﹣![]() ,
,![]() c)或C(
c)或C(![]() ,﹣
,﹣![]() c),
c),
∴点C在第四象限,c>0,
∴C(![]() ,﹣
,﹣![]() c),
c),
令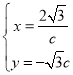 ,
,
∴xy=﹣6,即y=﹣![]() (x>0);
(x>0);
②当AG为平行四边形的边时,G与B重合时,为一临界点通过平移可求得C(1,﹣6),
∴yc≤﹣6;
当AG为平行四边形的对角线时,G与B重合时,求得C(3,﹣2),
G与A重合时,C(2,﹣3),
此时﹣3<yc≤﹣2,
综上所述:yc≤﹣6或﹣3<yc≤﹣2.

【题目】某学校八年级共400名学生,为了解该年级学生的视力情况,从中随机抽取40名学生的视力数据作为样本,数据统计如下:
4.2 4.1 4.7 4.1 4.3 4.3 4.4 4.6 4.1 5.2
5.2 4.5 5.0 4.5 4.3 4.4 4.8 5.3 4.5 5.2
4.4 4.2 4.3 5.3 4.9 5.2 4.9 4.8 4.6 5.1
4.2 4.4 4.5 4.1 4.5 5.1 4.4 5.0 5.2 5.3
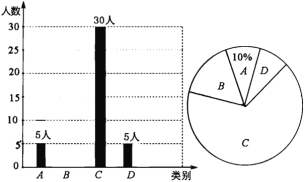
根据数据绘制了如下的表格和统计图:
等级 | 视力(x) | 频数 | 频率 |
|
| 4 | 0.1 |
|
| 12 | 0.3 |
|
|
| |
|
|
| |
| 10 | 0.25 | |
合计 | 40 | 1 | |
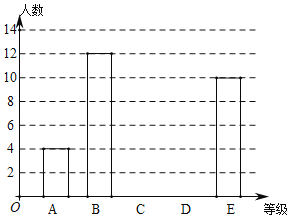
根据上面提供的信息,回答下列问题:
(1)统计表中的![]() ,
,![]() ;
;
(2)请补全条形统计图;
(3)根据抽样调查结果,请估计该校八年级学生视力为“![]() 级”的有多少人?
级”的有多少人?
(4)该年级学生会宣传部有2名男生和2名女生,现从中随机挑选2名同学参加“防控近视,爱眼护眼”宣传活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.