题目内容
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于A、B两点,直线y=
x2+bx+c与x轴交于A、B两点,直线y=![]() x+
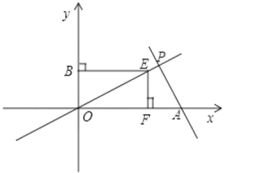
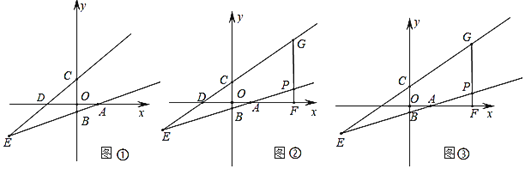
x+![]() 经过点A,与抛物线的另一个交点为点C(3,m),线段PQ在线段AB上移动,PQ=1,分别过点P、Q作x轴的垂线,交抛物线于E、F,交直线于D、G.
经过点A,与抛物线的另一个交点为点C(3,m),线段PQ在线段AB上移动,PQ=1,分别过点P、Q作x轴的垂线,交抛物线于E、F,交直线于D、G.
(1)求抛物线的解析式;
(2)设四边形DEFG的面积为S,求S的最大值;
(3)在线段PQ的移动过程中,以D,E,F,G为顶点的四边形是平行四边形时,求点P的坐标.
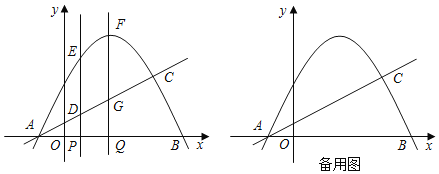
【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)当m=
x+2;(2)当m=![]() 时,S的最大值为:
时,S的最大值为:![]() ;(3)点P(1,0).
;(3)点P(1,0).
【解析】
(1)直线![]() 经过点A、C,则点A(-1,0)、(3,2),将点A、C的坐标代入抛物线表达式,即可求解;
经过点A、C,则点A(-1,0)、(3,2),将点A、C的坐标代入抛物线表达式,即可求解;
(2)由![]() ,即可求解;
,即可求解;
(3)线段PQ在线段AB上移动,出现平行四边形时,只能是在AC之上,即:DE=FG,即可求解.
解:(1)直线y=![]() x+
x+![]() 经过点A、C,则点A(﹣1,0)、(3,2),
经过点A、C,则点A(﹣1,0)、(3,2),
将点A、C的坐标代入抛物线表达式得: ,
,
解得:![]() ,
,
故抛物线的表达式为:y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)设点P(m,0),则点Q(m+1,0),D(m,m+![]() ),点G(m+1,
),点G(m+1,![]() m+1),点E(m,﹣
m+1),点E(m,﹣![]() m2+
m2+![]() m+2)、点F(m+1,﹣
m+2)、点F(m+1,﹣![]() m2+m+3),
m2+m+3),
S=![]() (DE+FG)×PQ
(DE+FG)×PQ
![]()
![]()
∵![]() ,
,
故S有最大值,当m=![]() 时,S的最大值为:
时,S的最大值为:![]() ;
;
(3)线段PQ在线段AB上移动,出现平行四边形时,只能是在AC之上,
即:DE=FG,由(2)得:![]() ,
,
解得:m=1,
即点P(1,0).

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目