Question

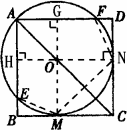
已知，O为正方形ABCD对角线上一点，以O为圆心，OA的长为半径的⊙O与BC相切于M，与AB、AD分别相交于E、F．

(1)求证：CD与⊙O相切．

(2)若正方形ABCD的边长为1，求⊙O的半径．

(3)对于以点M、E、A、F以及CD与O⊙的切点为顶点的五边形的五条边，从相等的关系考虑，你可以得出什么结论？请你给出证明

Answer 1

答案：
解析：

(1)连结OM，作ON⊥CD于N 　　∵⊙O与BC相切∴OM⊥BC 　　∵四边形ABCD是正方形∴AC平分∠BCD 　　∴OM＝ON∴CD与⊙O相切 　　(2)∵四边形ABCD是正方形 　　∴AD＝CD＝1，∠D＝90°，∠ACD＝45° 　　∴AC＝，∠NOC＝45°＝∠ACD 　　∴NC＝OC＝OA∴OC＝＝ON＝OA 　　∵AC＝AO＋OC＝∴AO＋AO＝∴OA＝2－ 　　(3)ME＝FN，AE＝AF 　　证明：作OG⊥AD，OH⊥AB 　　∵AC平分∠BAD∴OG＝OH∴AE＝AF 　　∵AD＝AB∴DF＝BE 　　∵CD、CB与⊙O相切∴CM＝CN∵BC＝DC∴BM＝DN 　　又∵∠B＝∠D＝90°∴△EBM≌△FDN∴EM＝FN