题目内容
9、如图，已知点E为正方形ABCD的边BC上一点，连接AE，过点D作DG⊥AE，垂足为G，延长DG交AB于点F．求证：BF=CE．分析：要证明BF=CE，只要证明AF=BE即可，可通过证明△AFD≌△BEA得到．
解答：证明：在正方形ABCD中，∠DAF=∠ABE=90°，DA=AB=BC，
∵DG⊥AE，
∴∠FDA+∠DAG=90°．
又∵∠EAB+∠DAG=90°，
∴∠FDA=∠EAB．
在Rt△DAF与Rt△ABE中，DA=AB，∠FDA=∠EAB，
∴Rt△DAF≌Rt△ABE．
∴AF=BE．
∵AB=BC，
∴BF=CE．
∵DG⊥AE，
∴∠FDA+∠DAG=90°．
又∵∠EAB+∠DAG=90°，
∴∠FDA=∠EAB．
在Rt△DAF与Rt△ABE中，DA=AB，∠FDA=∠EAB，
∴Rt△DAF≌Rt△ABE．
∴AF=BE．
∵AB=BC，
∴BF=CE．
点评：此题考查简单的线段相等，可以通过全等三角形来证明，要注意利用此题中的图形条件，同角的余角相等．
练习册系列答案
名校课堂系列答案
相关题目
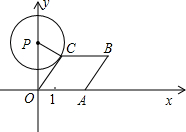A为顶点作菱形OABC，使点B，C在第一象限内，且∠AOC=60°；以P（0，3）为圆心，PC为半径作圆．设点A运动了t秒，求：
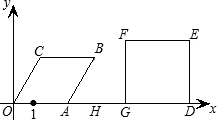，求出t的值；若不存在，请说明理由．
1个单位的速度向正方向运动，连接AP并延长，交抛物线于点B，分别过点A、B作x轴的垂线，垂足为C、D，连接AQ、BQ．
x2+c的图象上，点P从抛物线的顶点Q出发，沿y轴以每秒1个单位的速度向正方向运动，连结AP并延长，交抛物线于点B，分别过点A、B作x轴的垂线，垂足为C、D，连结AQ、BQ．
x2+c的图象上，点P从抛物线的顶点Q出发，沿y轴以