题目内容
20、如图，已知点E为正方形ABCD的边BC上一点，连接AE，过点D作DG⊥AE，垂足为G，延长DG交AB于点F．求证：AF=BE．
分析：根据正方形的性质得到AD=AB，∠CDA=∠DAB=∠B=90°，根据垂线和三角形的内角和定理求出∠ADG+∠DAG=90°，推出∠ADG=∠EAB，根据ASA推出△ADF≌△BAE即可．
解答：证明：∵正方形ABCD，
∴AD=AB，∠CDA=∠DAB=∠B=90°，
∵DG⊥AE，
∴∠DGA=90°，
∴∠ADG+∠DAG=90°，
∵∠ADG+∠EAB=90°，
∴∠ADG=∠EAB，
∵AD=AB，∠DAF=∠B=90°，
∴△ADF≌△BAE，
∴AF=BE．
∴AD=AB，∠CDA=∠DAB=∠B=90°，
∵DG⊥AE，
∴∠DGA=90°，
∴∠ADG+∠DAG=90°，
∵∠ADG+∠EAB=90°，
∴∠ADG=∠EAB，
∵AD=AB，∠DAF=∠B=90°，
∴△ADF≌△BAE，
∴AF=BE．
点评：本题主要考查对正方形的性质，三角形的内角和定理，垂线，全等三角形的性质和判定等知识点的理解和掌握，证出△ADF≌△BAE是解此题的关键．
练习册系列答案
相关题目
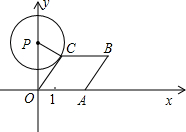A为顶点作菱形OABC，使点B，C在第一象限内，且∠AOC=60°；以P（0，3）为圆心，PC为半径作圆．设点A运动了t秒，求：
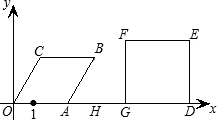，求出t的值；若不存在，请说明理由．
1个单位的速度向正方向运动，连接AP并延长，交抛物线于点B，分别过点A、B作x轴的垂线，垂足为C、D，连接AQ、BQ．
x2+c的图象上，点P从抛物线的顶点Q出发，沿y轴以每秒1个单位的速度向正方向运动，连结AP并延长，交抛物线于点B，分别过点A、B作x轴的垂线，垂足为C、D，连结AQ、BQ．
x2+c的图象上，点P从抛物线的顶点Q出发，沿y轴以