Question

已知，O为正方形ABCD对角线上一点，以O为圆心，OA的长为半径的⊙O与BC相切于M，与AB、AD分别相交于E、F．
（1）求证：CD与⊙O相切；
（2）若⊙O的半径为

2

，求正方形ABCD的边长．

Answer 1

分析：（1）连接OM，过O作ON于CD垂直，由BC与圆O相切，根据切线性质得到OM与BC，又正方形ABCD，AC为角平分线，根据角平分线定理得到OM=ON，故CD与圆O相切；
（2）根据垂直于同一条直线的两直线平行得到OM与AB平行，得到两对同位角相等，从而得到△ABC∽△OMC，设正方形的边长为a，由圆O的半径，列出比例式得到关于a的方程，求出方程的解得到a的值即为正方形的边长．

解答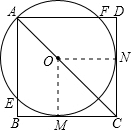：（1）证明：连接OM，过点O作ON⊥CD，垂足为N．（1分）
∵⊙O与BC相切于M，∴OM⊥BC．（2分）
∵正方形ABCD中，AC平分∠BCD，∴OM=ON．（3分）
∴CD与⊙O相切；（4分）

（2）解：设正方形ABCD的边长为a．
显然OM∥AB，∴∠OMC=∠B，∠MOC=∠BAC，
∴△COM∽△CAB，（5分）
∴

OM

AB

=

CO

CA

，即

2

a

=

2 a- 2

2 a

（6分）
解得a=

2

+1，（7分）
∴正方形ABCD的边长为

2

+1．

点评：此题考查了切线的性质与判断，正方形的性质以及相似三角形的性质与判断．其中切线的证明方法有两种：1、已知点，连接此点与圆心，证明夹角为直角；2、未知点，作垂线，证明垂线段等于半径．