题目内容
【题目】抛物线C1:y=a(x+1)(x﹣3a)(a>0)与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,﹣3)
(1)求抛物线C1的解析式及A,B点坐标;
(2)求抛物线C1的顶点坐标;
(3)将抛物线C1向上平移3个单位长度,再向左平移n(n>0)个单位长度,得到抛物线C2 , 若抛物线C2的顶点在△ABC内,求n的取值范围. (在所给坐标系中画出草图C1)
【答案】
(1)解:∵抛物线C1:y=a(x+1)(x﹣3a)y轴交于点C(0,﹣3),
∴﹣3=a(0+1)(0﹣3a),
解得a=1(舍去负值).
∴抛物线C1的解析式为:y=(x+1)(x﹣3).
∴A(﹣1,0),B(3,0)
(2)解:∵y=(x+1)(x﹣3)=(x﹣1)2﹣4,
∴该抛物线的解析式为y=(x﹣1)2﹣4,则该抛物线的顶点坐标为(1,﹣4)
(3)解:将(1)中求得的抛物线向上平移3个单位长度,
再向左平移n(n>0)个单位长度得到新抛物线y=(x﹣1+n)2﹣1,
∴平移后抛物线的顶点坐标是(1﹣n,﹣1),
∴﹣ ![]() <1﹣n<2,
<1﹣n<2,
解得﹣1<n< ![]() ,
,
∵n>0,
∴0<n< ![]() .
.
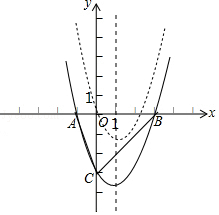
【解析】(1)根据已知点的坐标代入已知的函数的解析式即可利用待定系数法确定二次函数的解析式;(2)由(1)中的函数解析式即可求出抛物线C1的顶点坐标;(3)首先根据平移确定平移后的函数的解析式,然后确定抛物线C2的顶点坐标;结合图形确定n的取值范围即可.
【考点精析】利用二次函数图象的平移和抛物线与坐标轴的交点对题目进行判断即可得到答案,需要熟知平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案