题目内容
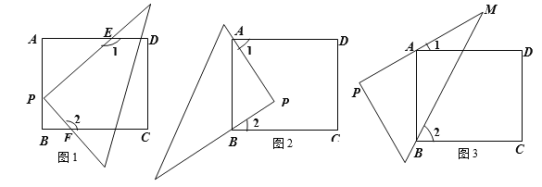
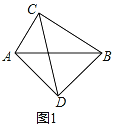
【题目】问题背景：如图（1）在四边形ABCD中，∠ACB=∠ADB=90°，AD=BD，探究线段AC、BC、CD之间的数量关系．小明探究此问题的思路是：将△BCD绕点D逆时针旋转90°到△AED处，点B、C分别落在点A、E处（如图（2）），易证点C、A、E在同一条直线上，并且△CDE是等腰直角三角形，所以CE=
CD，从而得出结论：AC+BC=CD．
简单应用：
（1）在图（1）中，若AC=，BC=2，求CD的长；
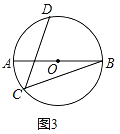
（2）如图（3）AB是⊙O的直径，点C、D在⊙O上，AD=BD，若AB=13，BC=12，求CD的长．
【答案】（1）3；（2）
.
【解析】分析: （1）代入结论：
，直接计算即可；
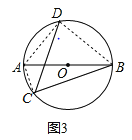
（2）如图3，作辅助线，根据直径所对的圆周角是直角得：
，由弧相等可知所对的弦相等，得到满足图1的条件，所以代入可得CD的长；
详解: (1)由题意知：
∴
∴CD=3；
故答案为：3；
(2)如图3，连接AC、BD、AD，
∵AB是⊙O的直径，
∴
∵弧AD=弧BD，
∴AD=BD，
∵AB=13，BC=12，
∴由勾股定理得：AC=5，
由图1得：
练习册系列答案
活力课时同步练习册系列答案
相关题目
