Question

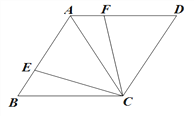
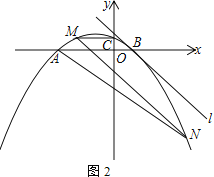
【题目】已知：抛物线y＝a(x－m)(x＋3m)（a＜0，m＞0）与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，直线l：y＝kx＋b经过点B，且与该抛物线有唯一公共点，平移直线l交抛物线于M、N两点（点M、N分别位于x轴上方和下方）

(1) 若，C(0，)

① 求该抛物线的解析式

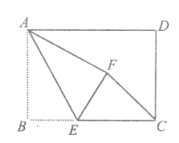
② 如图1，连接AM、AN，求证：∠MAB＝∠NAB

(2) 如图2，连接MC．若MC∥x轴，求的值

Answer 1

【答案】（1）①；② 证明见解析；（2）

【解析】（1）①利用a的值和点C的坐标，代入求解即可得到函数的解析式；

②过点M作MD⊥x轴于D，过点N作NE⊥x轴于E，由一次函数和二次函数的解析式联立方程组求参数的值，然后得出直线MN，联立方程组求出AD·NE－AE·MD=0，证明△MDA∽△NEA即可得解；

（2）设直线l：y＝kx＋b，联立方程组，化简后通过一元一次方程的根的判别式和线段的长求出比例即可.

(1) ① 当时，

将C(0，)代入中，得，m＝±1

∵m＞0

∴m＝1

∴

② 过点M作MD⊥x轴于D，过点N作NE⊥x轴于E

设直线l：y＝kx－k，M(x1，y1)、N(x2，y2)

联立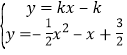，整理得

∵直线l与抛物线只有一个公共点

∴△＝4(k＋2)2＝0，解得k＝－2

设直线MN：y＝－2x＋t

联立，整理得x2－2x＋2t－3＝0

∴x1＋x2＝2，x1x2＝2t－3

∴AD·NE－AE·MD＝(x1＋3)(－y2)－(x2＋3)y1＝4x1x2＋(6－t)(x1＋x2)－6t

＝4(2t－3)＋(6－t)·2－6t＝0

∴AD·NE＝AE·MD

即

又∠MDA＝∠NEA＝90°

∴△MDA∽△NEA

∴∠MAB＝∠NAB

(2) y＝a(x2＋2mx－3m2)＝ax2＋2amx－3am2

设直线l：y＝kx＋b

将B(m，0)代入y＝kx＋b得，km＋b＝0，b＝－km

∴y＝kx－km

联立，整理得ax2＋(2am－k)x－3am2＋km＝0

∴△＝(2am－k)2－4a(－3am2＋km)＝0，得k＝4am

∴直线l：y＝4amx－4am2

∴M(－2m，－3am2)

∴直线MN的解析式为：y＝4amx＋5am2

联立，整理得ax2－2amx－8am2＝0

∴xM·xN＝－8m2

又xM＝－2m

∴xN＝4m

∴N(4m，21am2)

∴AM2＝m2＋9a2m4，AN2＝49m2＋212a2m4

∴，.