题目内容
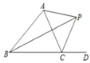
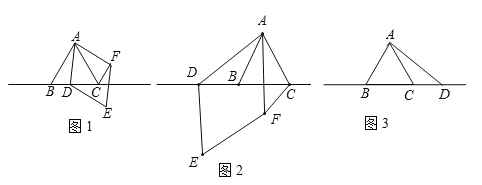
【题目】如图,已知∠DAE+∠CBF=180°,CE平分∠BCD,∠BCD=2∠E.
(1)求证:AD∥BC;
(2)CD与EF平行吗?写出证明过程;
(3)若DF平分∠ADC,求证:CE⊥DF.
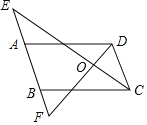
【答案】(1)详见解析;(2)CD∥EF,证明详见解析;(3)详见解析.
【解析】
(1)根据同角的补角相等,即可得到∠CBF=∠DAB,进而得到AD∥BC;
(2)依据∠BCD=2∠DCE,∠BCD=2∠E,即可得出∠E=∠DCE,进而判定CD∥EF;
(3)依据AD∥BC,可得∠ADC+∠DCB=180°,进而得到∠COD=90°,即可得出CE⊥DF.
解:(1)∵∠DAE+∠CBF=180°,∠DAE+∠DAB=180°,
∴∠CBF=∠DAB,
∴AD∥BC;
(2)CD与EF平行.
∵CE平分∠BCD,
∴∠BCD=2∠DCE,
又∵∠BCD=2∠E,
∴∠E=∠DCE,
∴CD∥EF;
(3)∵DF平分∠ADC,
∴∠CDF=![]() ∠ADC,
∠ADC,
∵∠BCD=2∠DCE,
∴∠DCE=![]() ∠DCB,
∠DCB,
∵AD∥BC,
∴∠ADC+∠DCB=180°,
∴∠CDF+∠DCE=![]() (∠ADC+∠DCB)=90°,
(∠ADC+∠DCB)=90°,
∴∠COD=90°,
∴CE⊥DF.

【题目】光明中学组织全校1000名学生进行了校园安全知识竞赛.为了解本次知识竞赛的成绩分布情况,从中随机抽取了部分学生的成绩(得分取正整数,满分为100分),并绘制了如图的频数分布表和频数分布直方图(不完整).
分组 | 频数 | 频率 |
50.5~60.5 | 10 | a |
60.5~70.5 | b | |
70.5~80.5 | 0.2 | |
80.5~90.5 | 52 | 0.26 |
90.5~100.5 | 0.37 | |
合计 | c | 1 |
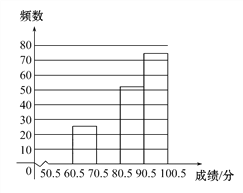
请根据以上提供的信息,解答下列问题:
(1)直接写出频数分布表中a,b,c的值,补全频数分布直方图.
(2)上述学生成绩的中位数落在哪一组范围内?
(3)学校将对成绩在90.5~100.5分之间的学生进行奖励,请估计全校1000名学生中约有多少名获奖?