ЬтФПФкШн
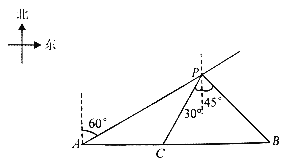
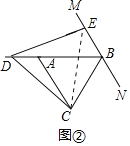
ЁОЬтФПЁПШчЭМЃЌЁїABCЪЧЕШБпШ§НЧаЮЃЌЙ§ЕуBзїMNЁЮACЃЌDЪЧЩфЯпBAЩЯЕФЖЏЕуЃЌЩфЯпDCШЦЕуDФцЪБеыа§зЊ60ЁуЕУЩфЯпDEЃЌDEНЛMNгкEЃЎ
ЃЈ1ЃЉШчЭМЂйЃЌЕБDЮЊABжаЕуЪБЃЌЧѓжЄЃКBD+BEЃНBCЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌЕБDдкBAбгГЄЯпЩЯЪБЃЌЃЈ1ЃЉЕФНсТлЪЧЗёГЩСЂЃПШєГЩСЂЃЌЧыжЄУїЃЛШєВЛГЩСЂЃЌЧыаДГіBCЃЌBDЃЌBEШ§ЬѕЯпЖЮЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЕБЁЯDCAЃН15ЁуЪБЃЌжБНгаДГіBDЃЌBEЕФЪ§СПЙиЯЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉНсТлВЛГЩСЂЃЎBDЉBEЃНBCЃЌМћНтЮіЃЛЃЈ3ЃЉBDЃНЃЈ1+![]() ЃЉBEЛђBDЃНЃЈ
ЃЉBEЛђBDЃНЃЈ![]() +
+![]() ЃЉBE
ЃЉBE
ЁОНтЮіЁП
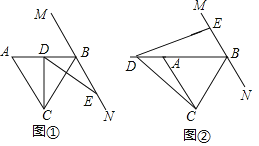
ЃЈ1ЃЉШчЭМ1жаЃЌСЌНгECЃЎЪзЯШжЄУїCЃЌDЃЌBЃЌEЫФЕуЙВдВЃЌЭЦГіЁїDCEЪЧЕШБпШ§НЧаЮЃЌдйжЄУїЁїACDЁеЁїBCEЃЈSASЃЉПЩЕУНсТлЃЎ
ЃЈ2ЃЉШчЭМ2жаЃЌНсТлВЛГЩСЂЃЎBDЉBEЃНBCЃЎжЄУїЗНЗЈРрЫЦЃЈ1ЃЉЃЌРћгУШЋЕШШ§НЧаЮЕФаджЪНтОіЮЪЬтМДПЩЃЎ
ЃЈ3ЃЉЗжСНжжЧщаЮЃКЂйШчЭМЂлЉ1жаЃЌЕБЕуDдкЯпЖЮABЩЯЪБЃЌНсТлЃКBDЃНЃЈ1+![]() ЃЉBEЃЎЂкШчЭМЂлЉ2жаЃЌЕБЕуDдкBAЕФбгГЄЯпЩЯЪБЃЌНсТлЃКBDЃНЃЈ
ЃЉBEЃЎЂкШчЭМЂлЉ2жаЃЌЕБЕуDдкBAЕФбгГЄЯпЩЯЪБЃЌНсТлЃКBDЃНЃЈ![]() +
+![]() ЃЉBEЃЌРћгУВЮЪ§НтжБНЧШ§НЧаЮНтОіЮЪЬтМДПЩЃЎ
ЃЉBEЃЌРћгУВЮЪ§НтжБНЧШ§НЧаЮНтОіЮЪЬтМДПЩЃЎ
ЃЈ1ЃЉжЄУїЃКШчЭМ1жаЃЌСЌНгECЃЎ

ЁпЁїABCЪЧЕШБпШ§НЧаЮЃЌ
ЁрCAЃНCBЃНABЃЌЁЯACBЃНЁЯABCЃН60ЁуЃЌ
ЁпMNЁЮACЃЌ
ЁрЁЯCBEЃНЁЯACBЃН60ЁуЃЌ
ЁпЁЯCDEЃН60ЁуЃЌ
ЁрЁЯCDEЃНЁЯCBEЃН60ЁуЃЌ
ЁрCЃЌDЃЌBЃЌEЫФЕуЙВдВЃЌ
ЁрЁЯCEDЃНЁЯCBDЃН60ЁуЃЌ
ЁрЁїDCEЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯACBЃНЁЯDCEЃН60ЁуЃЌ
ЁрЁЯACDЃНЁЯBCEЃЌ
ЁрЁїACDЁеЁїBCEЃЈSASЃЉЃЌ
ЁрADЃНBEЃЌ
ЁпBCЃНABЃНAD+BDЃЌ
ЁрBCЃНBE+BDЃЎ
ЃЈ2ЃЉНтЃКШчЭМ2жаЃЌНсТлВЛГЩСЂЃЎBDЉBEЃНBCЃЎ
РэгЩЃКСЌНгECЃЎ
ЁпЁїABCЪЧЕШБпШ§НЧаЮЃЌ
ЁрCAЃНCBЃНABЃЌЁЯACBЃНЁЯABCЃНЁЯCABЃН60ЁуЃЌ
ЁпMNЁЮACЃЌ
ЁрЁЯEBAЃНЁЯCABЃН60ЁуЃЌ
ЁрЁЯEBCЃН120ЁуЃЌ
ЁпЁЯCDEЃН60ЁуЃЌ
ЁрЁЯCDE+ЁЯCBEЃН180ЁуЃЌ
ЁрCЃЌDЃЌEЃЌBЫФЕуЙВдВЃЌ
ЁрЁЯCEDЃНЁЯCBDЃН60ЁуЃЌ
ЁрЁїDCEЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯDCEЃНЁЯACBЃН60ЁуЃЌ
ЁрЁЯACDЃНЁЯBCEЃЌ
ЁрЁїACDЁеЁїBCEЃЈSASЃЉЃЌ
ЁрADЃНBEЃЌ
ЁпBCЃНABЃНBDЉAD
ЁрBCЃНBDЉBEЃЎ
ЃЈ3ЃЉНтЃКЂйШчЭМЂлЉ1жаЃЌЕБЕуDдкЯпЖЮABЩЯЪБЃЌНсТлЃКBDЃНЃЈ1+![]() ЃЉBEЃЎ
ЃЉBEЃЎ
РэгЩЃКзїBHЁЭDEгкHЃЌдкDEЩЯШЁвЛЕуKЃЌЪЙЕУDKЃНBKЃЌСЌНгBKЃЎ
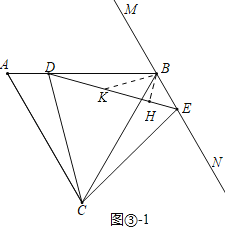
ЁпЁЯACDЃН15ЁуЃЌЁЯAЃНЁЯCDEЃН60ЁуЃЌЁЯBDCЃНЁЯA+ЁЯACDЃЌ
ЁрЁЯBDEЃНЁЯACDЃН60ЁуЃЌ
ЁпMNЁЮACЃЌ
ЁрЁЯCBNЃНЁЯACBЃН60ЁуЃЌ
ЁпЁЯABCЃН60ЁуЃЌ
ЁрЁЯDBEЃН120ЁуЃЌЁЯDEBЃН45ЁуЃЌ
ЁпBHЁЭDEЃЌ
ЁрЁЯBHEЃНЁЯBHDЃН90ЁуЃЌ
ЁрЁЯHBEЃНЁЯHEBЃН45ЁуЃЌ
ЁрBHЃНEHЃЌЩшBHЃНEHЃНxЃЌдђBEЃН![]() =
=![]() xЃЌ
xЃЌ
ЁпDKЃНKBЃЌ
ЁрЁЯKDBЃНЁЯKBDЃН15ЁуЃЌ
ЁрЁЯBKEЃНЁЯKDB+ЁЯKBDЃН30ЁуЃЌ
ЁрBKЃНDKЃН2xЃЌKHЃНBKcos30Ёу=![]() xЃЌ
xЃЌ
ЁрBDЃН![]() ЃН
ЃН![]() ЃНЃЈ
ЃНЃЈ![]() ЃЉxЃЌ
ЃЉxЃЌ
Ёр![]() ЃН
ЃН![]() ЃН1+
ЃН1+![]() ЃЌ
ЃЌ
ЁрBDЃНЃЈ1+![]() ЃЉBEЃЎ
ЃЉBEЃЎ
ЂкШчЭМЂлЉ2жаЃЌЕБЕуDдкBAЕФбгГЄЯпЩЯЪБЃЌНсТлЃКBDЃНЃЈ![]() +
+![]() ЃЉBEЃЌ
ЃЉBEЃЌ
РэгЩЃКзїEHЁЭABгкHЃЎ
дкDBЩЯШЁвЛЕуGЃЌЪЙЕУDGЃНEGЃЌСЌНгEGЃЎ
ЩшEHЃНmЃЎ
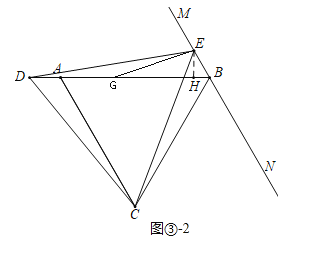
ЭЌЗЈПЩжЄЃКЁЯEDBЃН15ЁуЃЌЁЯEBHЃН60ЁуЃЌ
ЁрЁЯEGBЃН30ЁуЃЌ
дђгаDHЃНDG+GH=EG+GH=EHЁТsin30Ёу+EHЁТtan30Ёу=2m+![]() mЃЌEB=EHЁТsin60ЁуЃН
mЃЌEB=EHЁТsin60ЁуЃН![]() mЃЌ
mЃЌ
Ёр![]() ЃН
ЃН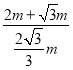 ЃН
ЃН![]() +
+![]()
ЁрBDЃНЃЈ![]() +
+![]() ЃЉBEЃЌ
ЃЉBEЃЌ

 ИпжаБиЫЂЬтЯЕСаД№АИ
ИпжаБиЫЂЬтЯЕСаД№АИЁОЬтФПЁПдкЩњЛюжаЃЌгаКмЖрКЏЪ§ВЂВЛвЛЖЈДцдкНтЮіЪНЃЌЖдгкетбљЕФКЏЪ§ЃЌЮвУЧПЩвдЭЈЙ§СаБэКЭЭМЯѓРДЖдЫќПЩФмДцдкЕФаджЪНјааЬНЫїЃЌР§ШчЯТУцетбљвЛИіЮЪЬтЃК
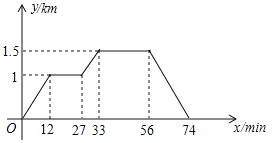
вбжЊyЪЧxЕФКЏЪ§ЃЌЯТБэЪЧyгыxЕФМИзщЖдгІжЕЃЎ
x | Ё | Љ5 | Љ4 | Љ3 | Љ2 | 0 | 1 | 2 | 3 | 4 | 5 | Ё |
y | Ё | 1.969 | 1.938 | 1.875 | 1.75 | 1 | 0 | Љ2 | Љ1.5 | 0 | 2.5 | Ё |
аЁЫяЭЌбЇИљОнбЇЯАКЏЪ§ЕФОбщЃЌРћгУЩЯЪіБэИёЗДгГГіЕФyгыxжЎМфЕФБфЛЏЙцТЩЃЌЖдИУКЏЪ§ЕФЭМЯѓгыаджЪНјааСЫЬНОПЃЎ
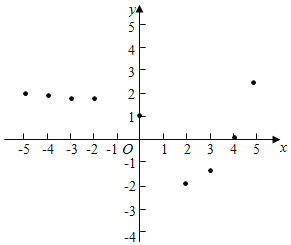
ЯТУцЪЧаЁЫяЭЌбЇЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећЃЛ
ЃЈ1ЃЉШчЭМЃЌдкЦНУцжЎМфзјБъЯЕxOyжаЃЌУшГіСЫвдЩЯБэжаИїЖдгІжЕЮЊзјБъЕФЕуЃЌИљОнУшГіЕФЕуЃЌЛГіКЏЪ§ЕФЭМЯѓЃК
ЃЈ2ЃЉИљОнЛГіЕФКЏЪ§ЭМЯѓЛиД№ЃК
ЂйxЃНЉ1ЪБЃЌЖдгІЕФКЏЪ§жЕyЕФЮЊЁЁ ЁЁЃЛ
ЂкШєКЏЪ§жЕyЃО0ЃЌдђxЕФШЁжЕЗЖЮЇЪЧЁЁ ЁЁЃЛ
ЂлаДГіИУКЏЪ§ЕФвЛЬѕаджЪЃЈВЛФмгыЧАУцвбгаЕФжиИДЃЉЃКЁЁ ЁЁЃЎ