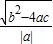题目内容
若m是关于x的一元二次方程x2+nx+m=0的根，且m≠0，则m+n的值为
- A.-1
- B.1
- C.
- D.
A
分析：根据一元二次方程的解的定义，将m代入关于x的一元二次方程x2+nx+m=0，通过解该方程即可求得m+n的值．
解答：∵m是关于x的一元二次方程x2+nx+m=0的根，
∴m2+nm+m=0，
∴m（m+n+1）=0；
又∵m≠0，
∴m+n+1=0，
解得，m+n=-1；
故选A．
点评：本题考查了一元二次方程的解的定义．一元二次方程ax2+bx+c=0（a≠0）的解一定满足该一元二次方程的关系式．
分析：根据一元二次方程的解的定义，将m代入关于x的一元二次方程x2+nx+m=0，通过解该方程即可求得m+n的值．
解答：∵m是关于x的一元二次方程x2+nx+m=0的根，
∴m2+nm+m=0，
∴m（m+n+1）=0；
又∵m≠0，
∴m+n+1=0，
解得，m+n=-1；
故选A．
点评：本题考查了一元二次方程的解的定义．一元二次方程ax2+bx+c=0（a≠0）的解一定满足该一元二次方程的关系式．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
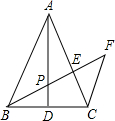（1997•吉林）已知△ABC中，∠A，∠B，∠C的对边分别是a，b，c，若a，b是关于x的一元二次方程x2-（c+4）x+4c+8=0的二根，且9c=25a•sinA．
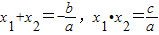．我们把它们称为根与系数关系定理．
=
=
=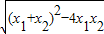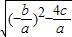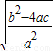