Question

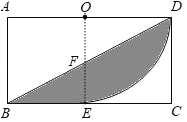
【题目】如图，矩形ABCD中，BC＝4，CD＝2，O为AD的中点，以AD为直径的弧DE与BC相切于点E，连接BD，则阴影部分的面积为（ ）

A.πB.C.π+2D.+4

Answer 1

【答案】A

【解析】

连接OE交BD于F，如图，利用切线的性质得到OE⊥BC，再证明四边形ODCE和四边形ABEO都是正方形得到BE=2，∠DOE=∠BEO=90°，易得△ODF≌△EBF，所以S△ODF=S△EBF，然后根据扇形的面积公式，利用阴影部分的面积=S扇形EOD计算即可．

连接OE交BD于F，如图，

∵以AD为直径的半圆O与BC相切于点E，

∴OE⊥BC．

∵四边形ABCD为矩形，OA=OD=2，

而CD=2，

∴四边形ODCE和四边形ABEO都是正方形，

∴BE=2，∠DOE=∠BEO=90°．

∵∠BFE=∠DFO，OD=BE，

∴△ODF≌△EBF(AAS)，

∴S△ODF=S△EBF，

∴阴影部分的面积=S扇形EOD．

故选：A．