题目内容
如图1,抛物线y=nx2-11nx+24n (n<0) 与x轴交于B、C两点(点B在点C的左侧),抛物线上另有一点A在第一象限内,且∠BAC=90°.
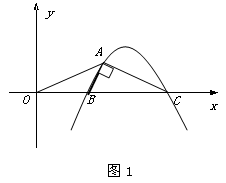
(1)填空:点B的坐标为(_ ),点C的坐标为(_ );
(2)连接OA,若△OAC为等腰三角形.
①求此时抛物线的解析式;
②如图2,将△OAC沿x轴翻折后得△ODC,点M为①中所求的抛物线上点A与点C两点之间一动点,且点M的横坐标为m,过动点M作垂直于x轴的直线l与CD交于点N,试探究:当m为何值时,四边形AMCN的面积取得最大值,并求出这个最大值.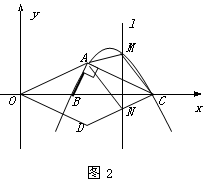

(1)填空:点B的坐标为(_ ),点C的坐标为(_ );
(2)连接OA,若△OAC为等腰三角形.
①求此时抛物线的解析式;
②如图2,将△OAC沿x轴翻折后得△ODC,点M为①中所求的抛物线上点A与点C两点之间一动点,且点M的横坐标为m,过动点M作垂直于x轴的直线l与CD交于点N,试探究:当m为何值时,四边形AMCN的面积取得最大值,并求出这个最大值.

解:(1)B(3,0),C(8,0)
(2)①作AE⊥OC,垂足为点E
∵△OAC是等腰三角形,∴OE=EC= ×8=4,∴BE=4-3=1
×8=4,∴BE=4-3=1
又∵∠BAC=90°,∴△ACE∽△BAE,∴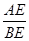 =
=
∴AE2=BE·CE=1×4,∴AE=2
∴点A的坐标为 (4,2)
把点A的坐标 (4,2)代入抛物线y=nx2-11nx+24n,得n=-
∴抛物线的解析式为y=- x2+
x2+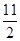 x-12
x-12
②∵点M的横坐标为m,且点M在①中的抛物线上
∴点M的坐标为 (m,- m2+
m2+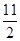 m-12),由①知,点D的坐标为(4,-2),
m-12),由①知,点D的坐标为(4,-2),
则C、D两点的坐标求直线CD的解析式为y= x-4
x-4
∴点N的坐标为 (m, m-4)
m-4)
∴MN m2+
m2+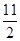 m-12)-(
m-12)-( m-4)=-
m-4)=- m2+5m-8
m2+5m-8
∴S四边形AMCN=S△AMN+S△CMN= MN·CE=
MN·CE= (-
(- m2+5m-8)×4=-(m-5)2+9
m2+5m-8)×4=-(m-5)2+9
∴当m=5时,S四边形AMCN=9
(2)①作AE⊥OC,垂足为点E
∵△OAC是等腰三角形,∴OE=EC=
 ×8=4,∴BE=4-3=1
×8=4,∴BE=4-3=1又∵∠BAC=90°,∴△ACE∽△BAE,∴
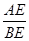 =
=
∴AE2=BE·CE=1×4,∴AE=2
∴点A的坐标为 (4,2)
把点A的坐标 (4,2)代入抛物线y=nx2-11nx+24n,得n=-

∴抛物线的解析式为y=-
 x2+
x2+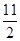 x-12
x-12 ②∵点M的横坐标为m,且点M在①中的抛物线上
∴点M的坐标为 (m,-
 m2+
m2+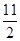 m-12),由①知,点D的坐标为(4,-2),
m-12),由①知,点D的坐标为(4,-2),则C、D两点的坐标求直线CD的解析式为y=
 x-4
x-4∴点N的坐标为 (m,
 m-4)
m-4)∴MN
 m2+
m2+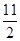 m-12)-(
m-12)-( m-4)=-
m-4)=- m2+5m-8
m2+5m-8 ∴S四边形AMCN=S△AMN+S△CMN=
 MN·CE=
MN·CE= (-
(- m2+5m-8)×4=-(m-5)2+9
m2+5m-8)×4=-(m-5)2+9 ∴当m=5时,S四边形AMCN=9
(1)根据二次函数与x轴交点坐标求法,解一元二次方程即可得出;
(2)①利用菱形性质得出AD⊥OC,则△ACE∽△BAE,即可得出A点坐标,进而求出二次函数解析式;
②首先求出过C、D两点的坐标的直线CD的解析式,进而利用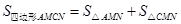 求出即可.
求出即可.
(2)①利用菱形性质得出AD⊥OC,则△ACE∽△BAE,即可得出A点坐标,进而求出二次函数解析式;
②首先求出过C、D两点的坐标的直线CD的解析式,进而利用
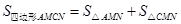 求出即可.
求出即可.
练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 x2+x-
x2+x-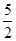 .
.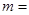 时,函数
时,函数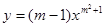 是二次函数。
是二次函数。
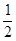 (x+1)2
(x+1)2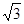 x2
x2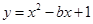 配方后为
配方后为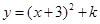 则
则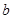 、
、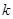 的值分别为( )
的值分别为( ) 的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是
的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是 ,则a+b+c=________.
,则a+b+c=________.