题目内容
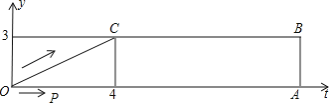
【题目】如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为(14,0)、(14,3)、(4,3).点P、Q同时从原点出发,分别作匀速运动,其中点P沿OA向终点A运动,速度为每秒1个单位;点Q沿OC、CB向终点B运动,当这两点中有一点到达自己的终点时,另一点也停止运动.设P从出发起运动了t秒.
(1)如果点Q的速度为每秒2个单位,①试分别写出这时点Q在OC上或在CB上时的坐标(用含t的代数式表示,不要求写出t的取值范围);
②求t为何值时,PQ∥OC?
(2)如果点P与点Q所经过的路程之和恰好为梯形OABC的周长的一半,①试用含t的代数式表示这时点Q所经过的路程和它的速度;
②试问:这时直线PQ是否可能同时把梯形OABC的面积也分成相等的两部分?如有可能,求出相应的t的值和P、Q的坐标;如不可能,请说明理由.
【答案】(1)①点Q在OC上时Q(![]() t,
t,![]() t),点Q在CB上时Q(2t﹣1,3);②t=5;(2)①v=
t),点Q在CB上时Q(2t﹣1,3);②t=5;(2)①v=![]() ,点Q所经过的路程为(16﹣t);②直线PQ不可能同时把梯形OABC的面积也分成相等的两部分.
,点Q所经过的路程为(16﹣t);②直线PQ不可能同时把梯形OABC的面积也分成相等的两部分.
【解析】
试题分析:(1)①根据相似三角形的性质即可求得点Q在OC上时的坐标;根据路程即可求得点Q在CB上时的横坐标是(2t﹣5),纵坐标和点C的纵坐标一致,是3;
②显然此时Q在CB上,由平行四边形的知识可得,只需根据OP=CQ列方程求解;
(2)①设Q的速度为v,根据P与点Q所经过的路程之和恰好为梯形OABC的周长的一半,即可建立函数关系式;
②显然Q应在CB上,根据面积和①中的结论得到关于t的方程,进行求解.
试题解析:(1)①点Q在OC上时Q(![]() t,
t,![]() t),点Q在CB上时Q(2t﹣1,3).
t),点Q在CB上时Q(2t﹣1,3).
②显然Q在CB上,由平行四边形的知识可得,只须OP=CQ.所以2t﹣5=t得t=5.
(2)①设Q的速度为v,先求梯形的周长为32,可得t+vt=16,所以v=![]() ,点Q所经过的路程为(16﹣t);
,点Q所经过的路程为(16﹣t);
②当Q在OC上时,做QM⊥OA,垂足为M,则QM=(16﹣t)×![]() ,∴S△OPQ=
,∴S△OPQ=![]() ×
×![]() (16﹣t)t=
(16﹣t)t=![]() t(16﹣t)=
t(16﹣t)=![]() S梯形OABC,则令
S梯形OABC,则令![]() t(16﹣t)=18,解得t1=10,t2=6,当t1=10时,16﹣x=6,此时点Q不在OC上,舍去;当t2=6时,16﹣x=10,此时点Q也不在OC上,舍去;∴当Q点在OC上时,PQ不可能同时把梯形OABC的面积也分成相等的两部分.
t(16﹣t)=18,解得t1=10,t2=6,当t1=10时,16﹣x=6,此时点Q不在OC上,舍去;当t2=6时,16﹣x=10,此时点Q也不在OC上,舍去;∴当Q点在OC上时,PQ不可能同时把梯形OABC的面积也分成相等的两部分.
当Q点在CB上时,CQ=16﹣t﹣5=11﹣x,∴S梯形OPQC=![]() ×(11﹣x+x)×3=
×(11﹣x+x)×3=![]() ≠18,∴当Q点在CB上时,PQ不可能同时把梯形OABC的面积也分成相等的两部分.
≠18,∴当Q点在CB上时,PQ不可能同时把梯形OABC的面积也分成相等的两部分.
综上所述,直线PQ不可能同时把梯形OABC的面积也分成相等的两部分.


【题目】二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x,y)对应值列表如下:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣3 | ﹣2 | ﹣3 | ﹣6 | ﹣11 | … |
则该函数图象的对称轴是( )
A.直线x=﹣3
B.直线x=﹣2
C.直线x=﹣1
D.直线x=0