题目内容
【题目】如图,正方形ABCD于正方形A1B1C1D1关于某点中心对称,已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标;
(2)写出顶点B,C,B1,C1的坐标.
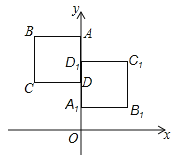
【答案】(1)(0,2.5);(2)分别是(﹣2,4),(﹣2,2),(2,1),(2,3).
【解析】
试题分析:(1)根据对称中心的性质,可得对称中心的坐标是D1D的中点,据此解答即可.
(2)首先根据A,D的坐标分别是(0,4),(0,2),求出正方形ABCD与正方形A1B1C1D1的边长是多少,然后根据A,D1,D三点的坐标分别是(0,4),(0,3),(0,2),判断出顶点B,C,B1,C1的坐标各是多少即可.
试题解析:(1)根据对称中心的性质,可得:对称中心的坐标是D1D的中点,∵D1,D的坐标分别是(0,3),(0,2),∴对称中心的坐标是(0,2.5);
(2)∵A,D的坐标分别是(0,4),(0,2),∴正方形ABCD与正方形A1B1C1D1的边长都是:4﹣2=2,∴B,C的坐标分别是(﹣2,4),(﹣2,2),∵A1D1=2,D1的坐标是(0,3),∴A1的坐标是(0,1),∴B1,C1的坐标分别是(2,1),(2,3),综上,可得:顶点B,C,B1,C1的坐标分别是(﹣2,4),(﹣2,2),(2,1),(2,3).

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
【题目】某校在国学文化进校园活动中,随机统计50名学生一周的课外阅读时间如表所示,
学生数(人) | 5 | 8 | 14 | 19 | 4 |
时间(小时) | 6 | 7 | 8 | 9 | 10 |
这组数据的众数和中位数分别是( )
A.14,9B.9,8C.9,9D.8,9