题目内容
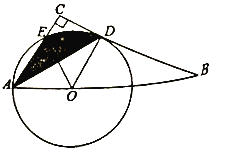
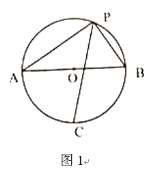
【题目】(1)已知:如图1,AB是![]() 的直径,点P为
的直径,点P为![]() 上一点(且点P不与A、B重合)连接PA,PB,
上一点(且点P不与A、B重合)连接PA,PB,![]() 的角平分线PC交
的角平分线PC交![]() 于点C.
于点C.
①若![]() ,求AB的长
,求AB的长
②求证:![]()
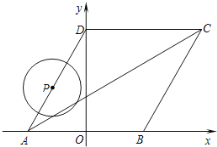
(2)如图2,在正方形ABCD中,![]() ,若点P满足
,若点P满足![]() ,且
,且![]() ,请直接写出点B到AP的距离.
,请直接写出点B到AP的距离.

【答案】(1)①![]() ,②见解析;(2)
,②见解析;(2)![]() 或
或![]()
【解析】
(1)①由AB是![]() 的直径,在Rt
的直径,在Rt![]() 中,利用勾股定理可求得AB的长;
中,利用勾股定理可求得AB的长;
②延长![]() 到
到![]() ,使
,使![]() ,构造
,构造![]()
![]() 和
和![]() 中,
中,
在同圆中利用圆周角相等,所对弧相等,所对的弦相等,证明![]() ,
,
利用圆内接四边形的一个外角等于不相邻的内角,证明![]() ,
,
BD=PA为所作,所以![]() (SAS)
(SAS)
从而证得:![]() ,
,
易证明![]() 是直角三角形,利用勾股定理可证明结论.
是直角三角形,利用勾股定理可证明结论.
(2)要满足![]() ,P点一定落在正方形的外接圆上,分两种情况:
,P点一定落在正方形的外接圆上,分两种情况:
P点在![]() 上或P点在
上或P点在![]() 上,
上,
在Rt![]() ABC和Rt
ABC和Rt![]() APC中,可求得AC、AP的长,
APC中,可求得AC、AP的长,
利用同圆中同弧所对圆周角相等,证得![]() ,
,
证得:Rt![]() QPB为等腰直角三角形,
QPB为等腰直角三角形,
设BQ=x,把已知和未知归结到Rt![]() QAB中,利用方程思想可以求得x的值.
QAB中,利用方程思想可以求得x的值.
(1)①![]() AB是
AB是![]() 的直径,∴
的直径,∴![]() ,
,
在Rt![]() 中,
中,![]() ,
,
∴![]() ,
,
故答案是:![]()
②如图,延长AB到D,使![]() ,连接
,连接![]()
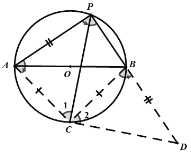
∵PC是![]() 的平分线,
的平分线,
∴![]() ,
,![]()
四边形APBC是圆内接四边形,
∴![]()
在![]() 和
和![]() 中,
中,
![]()
![]()
![]()
∴![]() (SAS)
(SAS)
∴![]() ,
,
∵![]()
∴![]() 即
即![]()
在Rt![]() 中,
中,![]()
即:![]()
∴![]()
(2)要满足![]() ,P点一定在正方形的外接圆上,分两种情况:
,P点一定在正方形的外接圆上,分两种情况:
第一种情况,P点在![]() 上,如图:连接
上,如图:连接![]() ,作
,作![]() ,
,
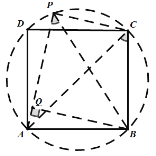
在![]() 中,
中,![]() ,∴AC=
,∴AC=![]() ,
,
在![]() 中,
中,![]() ,由勾股数可得:
,由勾股数可得:![]() ,
,
![]() ,
,
在![]() 中,
中,![]() , ∴
, ∴![]() ,
,
设![]() ,则
,则![]() ,
,
在![]() 中,
中,![]()
即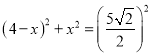 ,化简得:
,化简得:![]()
即![]() ,解得:
,解得:![]() ,
,![]() (不合题意,舍去)
(不合题意,舍去)
故答案为:![]() .
.
第二种情况,P点在![]() 上,如图:
上,如图:
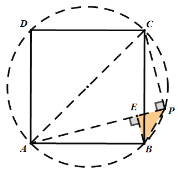
依照第一种情况得出的数据,![]()
![]()
在![]() 中,
中,![]() , ∴PE=BE,
, ∴PE=BE,
设![]() ,则
,则![]() ,
,
在![]() 中,
中,![]()
即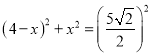 ,化简得:
,化简得:![]()
即![]() ,解得:
,解得:![]() (不合题意,舍去),
(不合题意,舍去),![]()
故答案为:![]() .
.
综上:点B到AP的距离是![]() 或
或![]() .
.

练习册系列答案
相关题目