Question

【题目】在平面直角坐标系xOy中，一次函数y=x+m的图象交y轴于点D，且它与正比例函数的图象交于点A（2，n），设x轴上有一点P，过点P作x轴的垂线（垂线位于点A的右侧），分别交和y=x+m的图象与点B、C.

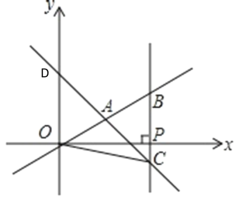
（1）求m和n的值；

（2）若BC=OD，求点P的坐标.

Answer 1

【答案】（1）m=3，；（2）（4,0）

【解析】

（1）将A（2，n）代入中即可求出n，然后再将A代入y=x+m即可求出m；

（2）设P点坐标为（a，0），然后分别表示出B、C两点的坐标，即可表示出BC的长，然后根据BC=OD列方程即可.

解：（1）将A（2，n）代入中，得：

，

再将A（2,1）代入y=x+m中，得：

1=2+m

解得：m=3

（2）设P点坐标为（a，0）

∵过点P作x轴的垂线（垂线位于点A的右侧），分别交和y=x+3的图象与点B、C

∴点B的坐标为，点C的坐标为：

∴BC=

把x=0代入y=x+3中，解得y=3

故点D的坐标为（0,3）

∴OD=3

∵BC=OD

∴

解得：

∴P点坐标为（4,0）