题目内容
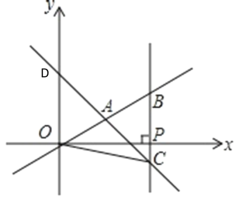
【题目】已知直线![]() 与
与![]() 交于A,B两点,且点A的横坐标为4,过原点O的另一条直线l交双曲线
交于A,B两点,且点A的横坐标为4,过原点O的另一条直线l交双曲线![]() 于P,Q两点(点P在第一象限),由点A,B,P,Q为顶点组成的四边形面积为24,则点P的坐标为_________.
于P,Q两点(点P在第一象限),由点A,B,P,Q为顶点组成的四边形面积为24,则点P的坐标为_________.
【答案】![]() 或(8,1)
或(8,1)
【解析】
作PM⊥y轴于M,PN⊥x轴于N,AH⊥x轴于H,设P点坐标为(a,b),先确定A点坐标为(4,2),再利用A点坐标确定反比例函数解析式为y=![]() ,根据反比例函数的性质可得到四边形APBQ为平行四边形,则根据平行四边形的性质得到S△OPA=
,根据反比例函数的性质可得到四边形APBQ为平行四边形,则根据平行四边形的性质得到S△OPA=![]() S平行四边形APBQ=6,由于S矩形ONPM+S梯形AHNP=S△OPM+S△OPA+S△OAH,化简反比例函数的比例系数的几何意义和梯形的面积公式有8+
S平行四边形APBQ=6,由于S矩形ONPM+S梯形AHNP=S△OPM+S△OPA+S△OAH,化简反比例函数的比例系数的几何意义和梯形的面积公式有8+![]() (2+b)(4-a)=4+6+4,再把b=
(2+b)(4-a)=4+6+4,再把b=![]() 代入得(2+
代入得(2+![]() )(4-a)=12,解得a1=2,a2=-8(舍去),当a=2,b=
)(4-a)=12,解得a1=2,a2=-8(舍去),当a=2,b=![]() =4,所以P点坐标为(2,4).
=4,所以P点坐标为(2,4).
作PM⊥y轴于M,PN⊥x轴于N,AH⊥x轴于H,如图,
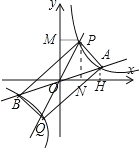
设P点坐标为(a,b)
把x=4代入y=![]() x得y=2,则A点坐标为(4,2),
x得y=2,则A点坐标为(4,2),
把A(4,2)代入y=![]() 得k=4×2=8,
得k=4×2=8,
所以反比例函数解析式为y=![]() ,
,
∵点A与点B关于原点对称,点P与点Q关于原点对称,
∴OA=OB,OP=OQ,
∴四边形APBQ为平行四边形,
∴S△OPA=![]() S平行四边形APBQ=
S平行四边形APBQ=![]() ×24=6,
×24=6,
∵S矩形ONPM+S梯形AHNP=S△OPM+S△OPA+S△OAH,
∴8+![]() (2+b)(4a)=4+6+4,
(2+b)(4a)=4+6+4,
∵b=![]() ,
,
∴(2+![]() )(4a)=12,
)(4a)=12,
整理得a2+6a16=0,解得a1=2,a2=8(舍去),
当a=2,b=![]() =4,
=4,
∴P点坐标为(2,4).
同理,当四边形BQPA是平行四边形时,点P的坐标是(8,1).
故答案为(2,4)或(8,1).

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目