题目内容
已知:如图,以等边三角形ABC一边AB为直径的⊙O与边AC、BC分别交于点D、E,过点D作DF⊥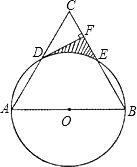 BC,垂足为F
BC,垂足为F(1)求证:DF为⊙O的切线;
(2)若等边三角形ABC的边长为4,求DF的长;
(3)求图中阴影部分的面积.
分析:(1)连接DO,要证明DF为⊙O的切线只要证明∠FDP=90°即可;
(2)由已知可得到CD,CF的长,从而利用勾股定理可求得DF的长;
(3)连接OE,求得CF,EF的长,从而利用S直角梯形FDOE-S扇形OED求得阴影部分的面积.
(2)由已知可得到CD,CF的长,从而利用勾股定理可求得DF的长;
(3)连接OE,求得CF,EF的长,从而利用S直角梯形FDOE-S扇形OED求得阴影部分的面积.
解答: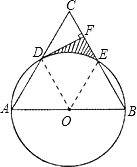 证明:(1)连接DO.
证明:(1)连接DO.
∵△ABC是等边三角形,
∴∠A=∠C=60°.
∵OA=OD,
∴△OAD是等边三角形.
∴∠ADO=60°,
∵DF⊥BC,
∴∠CDF=90°-∠C=30°,(2分)
∴∠FDO=180°-∠ADO-∠CDF=90°,
∴DF为⊙O的切线;(3分)
(2)∵△OAD是等边三角形,
∴AD=AO=
AB=2.
∴CD=AC-AD=2.
Rt△CDF中,
∵∠CDF=30°,
∴CF=
CD=1.
∴DF=
=
;(5分)
(3)连接OE,由(2)同理可知CE=2.
∴CF=1,
∴EF=1.
∴S直角梯形FDOE=
(EF+OD)•DF=
,
∴S扇形OED=
=
,
∴S阴影=S直角梯形FDOE-S扇形OED=
-
.(7分)
 证明:(1)连接DO.
证明:(1)连接DO.∵△ABC是等边三角形,
∴∠A=∠C=60°.
∵OA=OD,
∴△OAD是等边三角形.
∴∠ADO=60°,
∵DF⊥BC,
∴∠CDF=90°-∠C=30°,(2分)
∴∠FDO=180°-∠ADO-∠CDF=90°,
∴DF为⊙O的切线;(3分)
(2)∵△OAD是等边三角形,
∴AD=AO=
| 1 |
| 2 |
∴CD=AC-AD=2.
Rt△CDF中,
∵∠CDF=30°,
∴CF=
| 1 |
| 2 |
∴DF=
| CD2-CF2 |
| 3 |
(3)连接OE,由(2)同理可知CE=2.
∴CF=1,
∴EF=1.
∴S直角梯形FDOE=
| 1 |
| 2 |
3
| ||
| 2 |
∴S扇形OED=
| 60π×22 |
| 360 |
| 2π |
| 3 |
∴S阴影=S直角梯形FDOE-S扇形OED=
3
| ||
| 2 |
| 2π |
| 3 |
点评:此题考查学生对切线的判定及扇形的面积等知识点的掌握情况.

练习册系列答案
相关题目
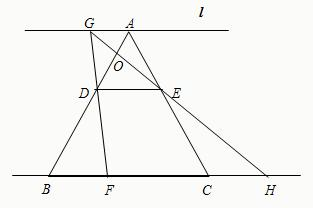 已知:如图,等边△ABC的边长为6,点D、E分别在AB、AC上,且AD=AE=2,直线l过点A,且l∥BC,若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动,设F点运动的时间为t秒,当t>0时,直线DF交l于点G,GE的延长线与BC的延长线交于点H,AB与GH相交于点O.
已知:如图,等边△ABC的边长为6,点D、E分别在AB、AC上,且AD=AE=2,直线l过点A,且l∥BC,若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动,设F点运动的时间为t秒,当t>0时,直线DF交l于点G,GE的延长线与BC的延长线交于点H,AB与GH相交于点O. 13、已知:如图,P是等边三角形ABC内部一点,且∠APC=117°,∠BPC=130°,
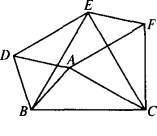
13、已知:如图,P是等边三角形ABC内部一点,且∠APC=117°,∠BPC=130°,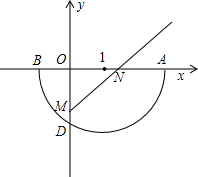 交于点D,顺次连接I、D、B三点可以组成等边三角形.过A、B两点的抛物线y=ax2+bx+c的顶点P也在半圆I上.
交于点D,顺次连接I、D、B三点可以组成等边三角形.过A、B两点的抛物线y=ax2+bx+c的顶点P也在半圆I上. 已知:如图所示,点C在线段AB上,分别以AC、BC为一边作为等边△ACM和等边△BCN,连接AN、BM.
已知:如图所示,点C在线段AB上,分别以AC、BC为一边作为等边△ACM和等边△BCN,连接AN、BM.