题目内容
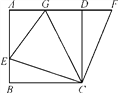
【题目】将一副三角板ABC和三角板BDE(∠ACB=∠DBE=90°,∠ABC=60°)按不同的位置摆放.

(1)如图1,若边BD,BA在同一直线上,则∠EBC= ;
(2)如图2,若∠EBC=165°,那么∠ABD= ;
(3)如图3,若∠EBC=120°,求∠ABD的度数。
【答案】(1)150°;(2)15°;(3)30°.
【解析】
(1)由∠EBC=∠DBE+∠ABC,可得结果;
(2)由∠ABD=∠CBE-∠ABC-∠DBE,可得结果;
(3)由∠ABD=∠ABC+∠DBE-∠EBC可得结果.
解:根据题意可知,
(1)∠EBC=∠DBE+∠ABC=90°+60°=150°;
故答案为:150°;
(2)∠ABD=∠CBE-∠ABC-∠DBE=165°-90°-60°=15°;
故答案为:15°;
(3)∠ABD=∠ABC+∠DBE-∠EBC=90°+60°-120°=30°.
∴∠ABD的度数为:30°.

练习册系列答案
相关题目
【题目】小龙在学校组织的社会调查活动中负责了解他所居住的小区450户居民的家庭收入情况、他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.

分组 | 频数 | 百分比 |
600≤x<800 | 2 | 5% |
800≤x<1000 | 6 | 15% |
1000≤x<1200 | 45% | |
9 | 22.5% | |
1600≤x<1800 | 2 | |
合计 | 40 | 100% |
根据以上提供的信息,解答下列问题:
(1)补全频数分布表;
(2)补全频数分布直方图;
(3)请你估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?