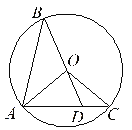题目内容
【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
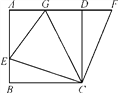
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
【答案】(1)证明见解析(2)GE=BE+GD成立
【解析】试题分析:(1)由DF=BE,四边形ABCD为正方形可证△CEB≌△CFD,从而证出CE=CF;
(2)由(1)得CE=CF,∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,又∠GCE=45°,所以可得∠GCE=∠GCF,故可证得△ECG≌△FCG,即EG=FG=GD+DF.又因为DF=BE,所以可证出GE=BE+GD成立.
试题解析:(1)∵在正方形ABCD中,BC=CD,∠B=∠CDF,BE=DF,
∴△CBE≌△CDF(SAS)
∴CE=CF.
(2)GE=BE+GD成立.
理由:由(1),得△CBE≌△CDF,
∴∠BCE=∠DCF,
∴∠BCE+∠ECD=∠DCF+∠ECD,即∠BCD=∠ECF=90°,
又∵∠GCE=45°,
∴∠GCF=∠GCE=45°,
∵CE=CF,∠GCE=∠GCF,GC=GC,
∴△ECG≌△FCG(SAS),
∴GE=GF,
∴GE=DF+GD=BE+GD.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】八年级(1)班张山同学利用所学函数知识,对函数![]() 进行了如下研究:
进行了如下研究:
列表如下:
x | … |
|
|
|
|
| 0 | 1 | 2 | 3 | … |
y | … | 7 | 5 | 3 | m | 1 | n | 1 | 1 | 1 | … |
描点并连线(如下图)
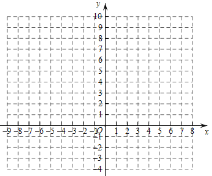
(1)自变量x的取值范围是________;
(2)表格中:![]() ________,
________,![]() ________;
________;
(3)在给出的坐标系中画出函数![]() 的图象;
的图象;
(4)一次函数![]() 的图象与函数
的图象与函数![]() 的图象交点的坐标为_______.
的图象交点的坐标为_______.