题目内容
【题目】 阅读:我们约定,在平面直角坐标系中,经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“特征线”.例如,点M(1,3)的特征线有:x=1,y=3,y=x+2,y=﹣x+4.
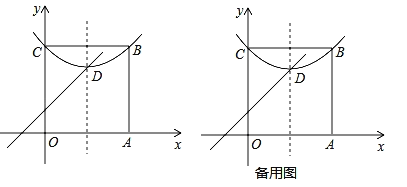
问题与探究:如图,在平面直角坐标系中有正方形OABC,点B在第一象限,A、C分别在x轴和y轴上,抛物线![]() 经过B、C两点,顶点D在正方形内部.
经过B、C两点,顶点D在正方形内部.
(1)直接写出点D(m,n)所有的特征线;
(2)若点D有一条特征线是y=x+1,求此抛物线的解析式;
(3)点P是AB边上除点A外的任意一点,连接OP,将△OAP沿着OP折叠,点A落在点A′的位置,当点A′在平行于坐标轴的D点的特征线上时,满足(2)中条件的抛物线向下平移多少距离,其顶点落在OP上?
【答案】(1)x=m,y=n,y=x+n﹣m,y=﹣x+m+n;(2)![]() ;(3)抛物线向下平移
;(3)抛物线向下平移![]() 或
或![]() 距离,其顶点落在OP上.
距离,其顶点落在OP上.
【解析】
试题(1)根据特征线直接求出点D的特征线;
(2)由点D的一条特征线和正方形的性质求出点D的坐标,从而求出抛物线解析式;
(2)分平行于x轴和y轴两种情况,由折叠的性质计算即可.
试题解析:解:(1)∵点D(m,n),∴点D(m,n)的特征线是x=m,y=n,y=x+n﹣m,y=﹣x+m+n;
(2)点D有一条特征线是y=x+1,∴n﹣m=1,∴n=m+1.∵抛物线解析式为![]() ,∴
,∴![]() ,∵四边形OABC是正方形,且D点为正方形的对称轴,D(m,n),∴B(2m,2m),∴
,∵四边形OABC是正方形,且D点为正方形的对称轴,D(m,n),∴B(2m,2m),∴![]() ,将n=m+1带入得到m=2,n=3;
,将n=m+1带入得到m=2,n=3;
∴D(2,3),∴抛物线解析式为![]() .
.
(3)①如图,当点A′在平行于y轴的D点的特征线时:
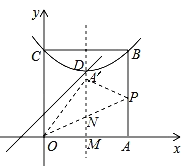
根据题意可得,D(2,3),∴OA′=OA=4,OM=2,∴∠A′OM=60°,∴∠A′OP=∠AOP=30°,∴MN=![]() =
=![]() ,∴抛物线需要向下平移的距离=
,∴抛物线需要向下平移的距离=![]() =
=![]() .
.
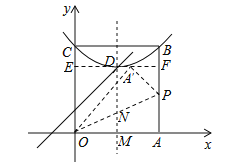
②如图,当点A′在平行于x轴的D点的特征线时,设A′(p,3),则OA′=OA=4,OE=3,EA′=![]() =
=![]() ,∴A′F=4﹣
,∴A′F=4﹣![]() ,设P(4,c)(c>0),,在Rt△A′FP中,(4﹣
,设P(4,c)(c>0),,在Rt△A′FP中,(4﹣![]() )2+(3﹣c)2=c2,∴c=
)2+(3﹣c)2=c2,∴c=![]() ,∴P(4,
,∴P(4,![]() ),∴直线OP解析式为y=
),∴直线OP解析式为y=![]() x,∴N(2,
x,∴N(2,![]() ),∴抛物线需要向下平移的距离=3﹣
),∴抛物线需要向下平移的距离=3﹣![]() =
=![]() .
.
综上所述:抛物线向下平移![]() 或
或![]() 距离,其顶点落在OP上.
距离,其顶点落在OP上.

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案