题目内容
【题目】△ABC中,∠ABC=45°,AB≠BC,BE⊥AC于点E,AD⊥BC于点D.
(1)如图1,作∠ADB的角平分线DF交BE于点F,连接AF.求证:∠FAB=∠FBA;
(2)如图2,连接DE,点G与点D关于直线AC对称,连接DG、EG
①依据题意补全图形;
②用等式表示线段AE、BE、DG之间的数量关系,并加以证明.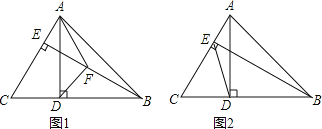
【答案】(1)见解析;(2)①见解析;②GD+AE=BE.理由见解析
【解析】
(1)欲证明∠FAB=∠FBA,由△ADF≌△BDF推出AF=BF即可解决问题.
(2)①根据条件画出图形即可.
②数量关系是:GD+AE=BE.过点D作DH⊥DE交BE于点H,先证明△ADE≌△BDH,再证明四边形GEHD是平行四边形即可解决问题.
(1)如图1中,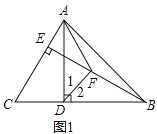
∵AD⊥BC,∠ABC=45°,
∴∠BAD=45°,
∴AD=BD,
∵DF平分∠ADB,
∴∠1=∠2,
在△ADF和△BDF中,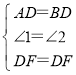 ,
,
∴△ADF≌△BDF.
∴AF=BF,
∴∠FAB=∠FBA.
(2)①补全图形如图2中所示,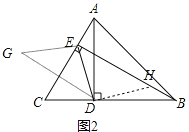
②数量关系是:GD+AE=BE.
理由:过点D作DH⊥DE交BE于点H
∴∠ADE+∠ADH=90°,
∵AD⊥BC,
∴∠BDH+∠ADH=90°,
∴∠ADE=∠BDH,
∵AD⊥BC,BE⊥AC,∠AKE=∠BKD,
∴∠DAE=∠DBH,
在△ADE和△BDH中,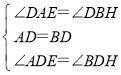 ,
,
∴△ADE≌△BDH.
∴DE=DH,AE=BH,
∵DH⊥DE,
∴∠DEH=∠DHE=45°,
∵BE⊥AC,
∴∠DEC=45°,∵点G与点D关于直线AC对称,
∴AC垂直平分GD,
∴GD∥BE,∠GEC=∠DEC=45°,
∴∠GED=∠EDH=90°,
∴GE∥DH,
∴四边形GEHD是平行四边形
∴GD=EH,
∴GD+AE=BE.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案【题目】二次函数图象上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | -4 | -3 | -2 | -1 | 0 | 1 | … |
| … | 5 | 0 | -3 | -4 | -3 | m | … |
(1)m= ;
(2)在图中画出这个二次函数的图象;
(3)当![]() 时,x的取值范围是 ;
时,x的取值范围是 ;
(4)当![]() 时,y的取值范围是 .
时,y的取值范围是 .