Question

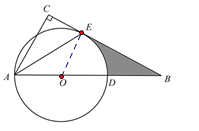
【题目】如图，在Rt△ABC中，∠C＝90°，点D在AB上，以AD为直径的⊙O与BC相

交于点E，且AE平分∠BAC．

（1）求证：BC是⊙O的切线；

（2）若∠EAB＝30°，OD＝3，求图中阴影部分的面积．

Answer 1

【答案】（1）证明见解析；（2）.

【解析】试题分析： 连接证明，从而得出∠OEB＝∠C＝90°，从而得证.

阴影部分的面积等于三角形的面积减去扇形的面积.

试题解析： 连接

∵AE平分∠BAC，

∴∠CAE＝∠EAD，

∵OA＝OE，

∴∠EAD＝∠OEA，

∴∠OEA＝∠CAE，

，

∴∠OEB＝∠C＝90°，

∴OE⊥BC，且点E在⊙O上，

∴BC是⊙O的切线．

（2）解： ∵∠EAB＝30°，

∴∠EOD＝60°，

∵∠OEB＝90°，

∴∠B＝30°，

∴OB＝2OE＝2OD＝6，

∴

扇形的面积

阴影部分的面积为：