Question

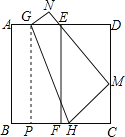
【题目】如图，将边长为6的正方形纸片ABCD对折，使AB与DC重合，折痕为EF，展平后，再将点B折到边CD上，使边AB经过点E，折痕为GH，点B的对应点为M，点A的对应点为N.

（1） 若CM=x，则CH= （用含x的代数式表示）；

（2）求折痕GH的长.

Answer 1

【答案】（1）；（2）.

【解析】试题分析： 利用翻折变换的性质结合勾股定理表示出的长即可；
首先得出，进而求出的长，再利用求出的长，再利用勾股定理得出的长．

试题解析：(1)∵CM=x，BC=6，

∴设HC=y，则BH=HM=6y，

故整理得：

故答案为：

(2)∵四边形ABCD为正方形，

设CM=x,由题意可得：

故

即

解得： (不合题意舍去)，

∴CM=2,

∴DM=4，

∴在中，由勾股定理得：EM=5，

解得：

由翻折变换的性质,得AG=NG=43，

过点G作GP⊥BC，垂足为P，

则当x=2时,

在中,