题目内容
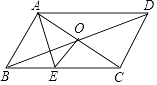
【题目】如图,在四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,求y与x之间的函数表达式.

【答案】y=![]()
![]() ·
·![]() x=
x=![]() x2
x2
【解析】试题分析:过D作DE⊥AC与E点,设BC=a,则AC=4a,根据等角的余角相等得到∠1=∠3,易证得△ABC≌△DAE,所以AE=BC=a,DE=AC=4a,得到EC=AC-AE=4a-a=3a,在Rt△DEC中,根据勾股定理得到DC=5a,所以有x=5a,即a= ![]() ;根据四边形ABCD的面积y=三角形ABC的面积+三角形ACD的面积,即可得到.
;根据四边形ABCD的面积y=三角形ABC的面积+三角形ACD的面积,即可得到.
试题解析:
过D作DE⊥AC于E点,如图,
设BC=a,则AC=4a,
∵∠BAD=90°,∠AED=90°,
∴∠1=∠3,
而∠ACB=90°,AB=AD,
∴△ABC≌△DAE,
∴AE=BC=a,DE=AC=4a,
∴EC=AC-AE=4a-a=3a,
在Rt△DEC中,DC=5a,
∴x=5a,即a= ![]() ,
,
又∵四边形ABCD的面积y=三角形ABC的面积+三角形ACD的面积,
∴![]() ,
,
即y与x之间的函数关系式是y=![]() .
.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目