Question

【题目】如图，平行四边形ABCD中，对角线AC，BD交于O，EO⊥AC，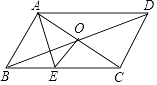
（1）若△ABE的周长为10cm，求平行四边形ABCD的周长，
（2）若∠DAB=108°，AE平分∠BAC，试求∠ACB的度数．

Answer 1

【答案】
（1）解：∵四边形ABCD是平行四边形，

∴OA=OC．

∵OE⊥AC，

∴AE=CE．

∴△ABE的周长为AB+AC=10，

根据平行四边形的对边相等得，

平行四边形ABCD的周长为2×10=20cm．

（2）解：∵AE平分∠BAC，

∴∠BAE=∠CAE，

∵△ACE是等腰三角形，

∴∠CAE=∠ACB

∵四边形ABCD是平行四边形，

∴∠ACB=∠CAD，

∴∠DAB=∠BAE+∠CAE+∠CAD=3∠CAD=108°，

∴∠ACB=∠CAD=36°．

【解析】（1）根据平行四边形的对角线互相平分得：OA=OC．又OE⊥AC，根据线段垂直平分线上的点到线段两个端点的距离相等得：AE=CE．故△ABE的周长为AB+BC的长．最后根据平行四边形的对边相等得：ABCD的周长为2×10=20cm．（2）由已知条件和平行四边形的性质易求∠DAB=∠BAE+∠CAE+∠CAD=3∠CAD=108°，进而可求出∠ACB的度数．
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识，掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分．