Question

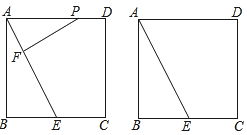
【题目】如图①，定义：在四边形ABCD中，若AD＝BC，且∠ADB＋∠BCA＝180°，则把四边形ABCD叫作互补等对边四边形．如图②，在等腰△ABE中，AE＝BE，四边形ABCD是互补等对边四边形．试说明：∠ABD＝∠BAC＝∠E.

Answer 1

【答案】证明见解析.

【解析】

已知AE＝BE，根据等腰三角形的性质可得∠EAB＝∠EBA.根据互补等对边四边形的定义可得AD＝BC.利用SAS证明△ABD≌△BAC，根据全等三角形的性质可得∠ABD＝∠BAC，∠ADB＝∠BCA；根据互补等对边四边形的定义可得∠ADB＋∠BCA＝180°，即可求得∠ADB＝∠BCA＝90°.在等腰△ABE中，根据等腰三角形的性质及三角形的内角和定理可得∠EAB＝∠EBA＝ (180°－∠E)＝90°－∠E，所以∠ABD＝90°－∠EAB＝90°－＝∠E，由此即可证得结论.

∵AE＝BE，

∴∠EAB＝∠EBA.

∵四边形ABCD是互补等对边四边形，

∴AD＝BC.

在△ABD与△BAC中，,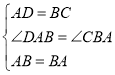

∴△ABD≌△BAC，

∴∠ABD＝∠BAC，∠ADB＝∠BCA.

∵∠ADB＋∠BCA＝180°，

∴∠ADB＝∠BCA＝90°.

在等腰△ABE中，∵∠EAB＝∠EBA＝ (180°－∠E)＝90°－∠E，

∴∠ABD＝90°－∠EAB＝90°－＝∠E，

∴∠ABD＝∠BAC＝∠E.