题目内容
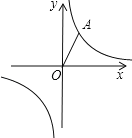
【题目】在平面直角坐标系中,已知反比例函数y=![]() 的图象经过点A,点O是坐标原点,OA=2且OA与x轴的夹角是60°.
的图象经过点A,点O是坐标原点,OA=2且OA与x轴的夹角是60°.
(1)试确定此反比例函数的解析式;
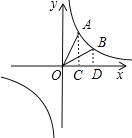
(2)将线段OA绕O点顺时针旋转30°得到线段OB,判断点B是否在此反比例函数的图象上,并说明理由.
【答案】(1)y=![]() ;(2)点B(
;(2)点B(![]() ,1)在反比例函数y=
,1)在反比例函数y=![]() 的图象上.
的图象上.
【解析】
试题分析:(1)作AC⊥x轴于点C,在Rt△AOC中,解直角三角形求得A点坐标为(1,![]() ),把A(1,
),把A(1,![]() )分别代入代入y=
)分别代入代入y=![]() ,根据待定系数法即可求得;
,根据待定系数法即可求得;
(2)作BD⊥x轴于点D,在Rt△BOD中,解直角三角形求得B点坐标为(![]() ,1),把x=
,1),把x=![]() 代入代入y=
代入代入y=![]() ,即可判断.
,即可判断.
解:(1)作AC⊥x轴于点C,如图,
在Rt△AOC中,
∵OA=2,∠AOC=60°,
∴∠OAC=30°,
∴OC=![]() OA=1,AC=
OA=1,AC=![]() OC=
OC=![]() ,
,
∴A点坐标为(1,![]() ),
),
把A(1,![]() )代入y=
)代入y=![]() ,
,
得k=1×![]() =
=![]() ,
,
∴反比例函数的解析式为y=![]() ;
;
(2)点B在此反比例函数的图象上,
理由如下:过点B作x轴的垂线交x轴于点D,
∵线段OA绕O点顺时针旋转30°得到线段OB,
∴∠AOB=30°,OB=OA=2,∴∠BOD=30°,
在Rt△BOD中,BD=![]() OB=1,OD=
OB=1,OD=![]() BD=
BD=![]() ,
,
∴B点坐标为(![]() ,1),
,1),
∵当x=![]() 时,y=
时,y=![]() =1,
=1,
∴点B(![]() ,1)在反比例函数y=
,1)在反比例函数y=![]() 的图象上.
的图象上.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目