题目内容
如图，在直角梯形ABCD中，AB∥DC，∠ADC=90°．AB=2，CD=3，AD=7．在腰AD上是否存在点P．使△ABP与△DCP相似？如果存在，试求出AP的长；如果不存在，试说明理由．
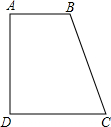
∵在直角梯形ABCD中，AB∥DC，∠ADC=90°，
∴∠DAB=∠ADC=90°，
若
=
，则△ABP∽△DCP，
∵AB=2，CD=3，
∴PA：PD=2：3，
∵AD=7，
∴AP=
AD=
；
若
=
，则△ABP∽△DPC，
∵AB=2，CD=3，
∴PA•PD=6，
∵AD=PA+PD=7，
设PA=x，则PD=7-x，
∴x（7-x）=6，
即x2-7x+6=0，
解得：x1=1，x2=6，
即PA=1或6；
∴AP的长为：
或1或6．
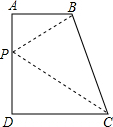
∴∠DAB=∠ADC=90°，
若
| PA |
| PD |
| AB |
| DC |
∵AB=2，CD=3，
∴PA：PD=2：3，
∵AD=7，
∴AP=
| 2 |
| 5 |
| 14 |
| 5 |
若
| PA |
| DC |
| AB |
| PD |
∵AB=2，CD=3，
∴PA•PD=6，
∵AD=PA+PD=7，
设PA=x，则PD=7-x，
∴x（7-x）=6，
即x2-7x+6=0，
解得：x1=1，x2=6，
即PA=1或6；
∴AP的长为：
| 14 |
| 5 |
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
