题目内容
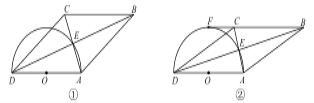
【题目】四边形 ABCD 的对角线交于点 E,且 AE=EC,BE=ED,以 AD 为直径的半圆过点 E,圆心 为 O.
(1)如图①,求证:四边形 ABCD 为菱形;
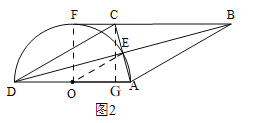
(2)如图②,若 BC 的延长线与半圆相切于点 F,且直径 AD=6,求弧AE 的长.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)先判断出四边形ABCD是平行四边形,再判断出AC⊥BD即可得出结论;
(2)先判断出AD=DC且DE⊥AC,∠ADE=∠CDE,进而得出∠CDA=30°,最后用弧长公式即可得出结论.
试题解析:证明:(1)∵四边形ABCD的对角线交于点E,且AE=EC,BE=ED,∴四边形ABCD是平行四边形.∵以AD为直径的半圆过点E,∴∠AED=90°,即有AC⊥BD,∴四边形ABCD 是菱形;
(2)由(1)知,四边形ABCD 是菱形,∴△ADC为等腰三角形,∴AD=DC且DE⊥AC,∠ADE=∠CDE.如图2,过点C作CG⊥AD,垂足为G,连接FO.∵BF切圆O于点F,∴OF⊥AD,且![]() ,易知,四边形CGOF为矩形,∴CG=OF=3.
,易知,四边形CGOF为矩形,∴CG=OF=3.
在Rt△CDG中,CD=AD=6,sin∠ADC=![]() =
=![]() ,∴∠CDA=30°,∴∠ADE=15°.
,∴∠CDA=30°,∴∠ADE=15°.
连接OE,则∠AOE=2×∠ADE=30°,∴![]() .
.

练习册系列答案
相关题目