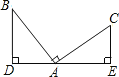
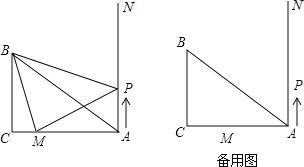
题目内容
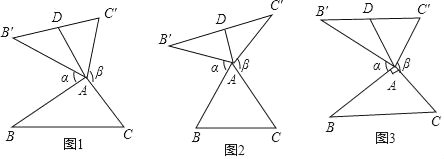
【题目】 我们定义:如图1、图2、图3,在△ABC中,把AB绕点A顺时针旋转α(0°<α<180°)得到AB′,把AC绕点A逆时针旋转β得到AC′,连接B′C′,当α+β=180°时,我们称△AB'C′是△ABC的“旋补三角形”,△AB′C′边B'C′上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.图1、图2、图3中的△AB′C′均是△ABC的“旋补三角形”.
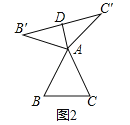
(1)①如图2,当△ABC为等边三角形时,“旋补中线”AD与BC的数量关系为:AD= BC;
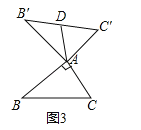
②如图3,当∠BAC=90°,BC=8时,则“旋补中线”AD长为 .
(2)在图1中,当△ABC为任意三角形时,猜想“旋补中线”AD与BC的数量关系,并给予证明.
【答案】(1)①![]() ;②4;(2)AD=
;②4;(2)AD=![]() BC.
BC.
【解析】
(1)①首先证明△ADB'是含有30°的直角三角形,可得AD![]() AB'即可解决问题;
AB'即可解决问题;
②首先证明△BAC≌△B'AC',根据直角三角形斜边中线定理即可解决问题;
(2)结论:AD![]() BC.如图1中,延长AD到M,使得AD=DM,连接B'M,C'M,首先证明四边形AC'MB'是平行四边形,再证明△BAC≌△AB'M,即可解决问题.
BC.如图1中,延长AD到M,使得AD=DM,连接B'M,C'M,首先证明四边形AC'MB'是平行四边形,再证明△BAC≌△AB'M,即可解决问题.
(1)①如图2中,∵△ABC是等边三角形,∴AB=BC=AC=AB'=AC'.
∵DB'=DC',∴AD⊥B'C'.
∵∠BAC=60°,∠BAC+∠B'AC'=180°,∴∠B'AC'=120°,∴∠B'=∠C'=30°,∴AD![]() AB'
AB'![]() BC.
BC.
故答案为:![]() .
.
②如图3中,∵∠BAC=90°,∠BAC+∠B'AC'=180°,∴∠B'AC'=∠BAC=90°.
∵AB=AB',AC=AC',∴△BAC≌△B'AC',∴BC=B'C'.
∵B'D=DC',∴AD![]() B'C'
B'C'![]() BC=4.
BC=4.
故答案为:4.
(2)结论:AD![]() BC.
BC.
理由:如图1中,延长AD到M,使得AD=DM,连接B'M,C'M.
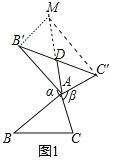
∵B'D=DC',AD=DM,∴四边形AC'MB'是平行四边形,∴AC'=B'M=AC.
∵∠BAC+∠B'AC'=180°,∠B'AC'+∠AB'M=180°,∴∠BAC=∠MB'A.
∵AB=AB',∴△BAC≌△AB'M,∴BC=AM,∴AD![]() BC.
BC.

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案