题目内容
【题目】如图,在△ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.
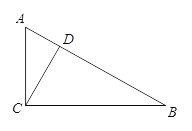
(1)求证:CD⊥AB;
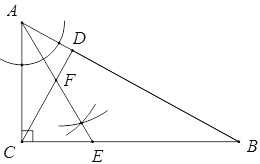
(2)在(1)中画△ABC的角平分线AE,交CD于点F,试判断∠AEC与∠CFE的数量关系,并说明理由.
【答案】(1)证明见解析;(2)画图见解析,∠AEC=∠CFE,理由见解析.
【解析】试题分析:(1)由∠ACB=90°,可得∠A+∠B=90°,由∠ACD=∠B,从而可得∠ACD+∠A=90°,继而∠ADC=90°,问题得证;
(2)利用尺规作图的方法作出角平分线AE,然后利用直角三角形两锐角互余,从而可得.
试题解析:(1)∵∠ACB=90°,∴∠A+∠B=90°,∵∠ACD=∠B,∴∠ACD+∠A=90°,∴∠ADC=90°,即CD⊥AB;
(2)如图所示;
∠AEC=∠CFE,理由如下:
∵∠ACE=90°,∴∠AEC+∠CAE=90°,∵∠ADC=90°,∴∠EAD+∠AFD=90°,∵∠CAE=∠EAD,∴∠AEC=∠AFD,∵∠CFE=∠AFD,∴∠AEC=∠ CFE.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】9岁的小芳身高1.36米,她的表姐明年想报考北京的大学.表姐的父母打算今年暑假带着小芳及其表姐先去北京旅游一趟,对北京有所了解.他们四人7月31日下午从无锡出发,1日到4日在北京旅游,8月5日上午返回无锡.
无锡与北京之间的火车票和飞机票价如下:火车 (高铁二等座) 全票524元,身高1.1~1.5米的儿童享受半价票;飞机 (普通舱) 全票1240元,已满2周岁未满12周岁的儿童享受半价票.他们往北京的开支预计如下:
住宿费 (2人一间的标准间) | 伙食费 | 市内交通费 | 旅游景点门票费 (身高超过1.2米全票) |
每间每天x元 | 每人每天100元 | 每人每天y元 | 每人每天120元 |
假设他们四人在北京的住宿费刚好等于上表所示其他三项费用之和,7月31日和8月5日合计按一天计算,不参观景点,但产生住宿、伙食、市内交通三项费用.
(1)他们往返都坐火车,结算下来本次旅游总共开支了13668元,求x,y的值;
(2)若去时坐火车,回来坐飞机,且飞机成人票打五五折,其他开支不变,他们准备了14000元,是否够用? 如果不够,他们准备不再增加开支,而是压缩住宿的费用,请问他们预定的标准间房价每天不能超过多少元?
【题目】一茶叶专卖店经销某种品牌的茶叶,该茶叶的成本价是80元/kg,销售单价不低于120元/kg.且不高于180元/kg,经销一段时间后得到如下数据:
销售单价x(元/kg) | 120 | 130 | … | 180 |
每天销量y(kg) | 100 | 95 | … | 70 |
设y与x的关系是我们所学过的某一种函数关系.
(1)直接写出y与x的函数关系式,并指出自变量x的取值范围;
(2)当销售单价为多少时,销售利润最大?最大利润是多少?