Question

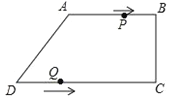
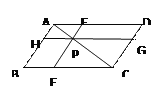
【题目】在□ABCD 中，点P在对角线AC上，过P作EF∥AB，HG∥AD，记四边形BFPH的面积为S1，四边形DEPG的面积为S2，则S1与S2的大小关系是（ ）

A. S1>S2 B. S1=S2 C. S1<S2 D. 无法判断

Answer 1

【答案】B

【解析】先证四边形ABPE和四边形PFCG都是平行四边形，再利用平行四边形对角线平分

四边形面积即可.

因为，在□ABCD 中，点P在对角线AC上，过P作EF∥AB，HG∥AD，

所以，四边形边形ABPE和四边形PFCG都是平行四边形，

所以，S△ABC=S△CDA,S△AEP=S△PHA,S△PFC=S△CGP,

所以，S△ABC- S△AEP - S△PFC =S△CDA- S△PHA- S△CGP,

所以，S△BFPH=S△DEPG，即：S1=S2

故选：B