Question

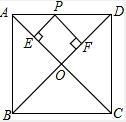
如图，正方形ABCD边长为4，点P在边AD上，且PE⊥AC，PF⊥BD，垂足分别为E、F，则PE+PF的值为______．

Answer 1

∵正方形ABCD边长为4，
∴AD=CD=4，AC⊥BD，
∴∠DAO=45°；
∴AC²=AD²+CD²=4²+4²=32，则AC=4

2

，
∵PE⊥AC，PF⊥BD，
∴∠PEC=∠PFB=90°；
又∵AC⊥BD，
∴四边形EPFO是矩形；
∴PF=OE，
又∵∠DAO=∠APE=45°，
∴AE=PE；
∵AE+OE=OA=

1

2

AC=

1

2

×4

2

=2

2

，
∴PE+PF=2

2

．
故答案为2

2

．