题目内容
【题目】如图,点P是矩形ABCD的边AD的一个动点,矩形的两条边AB、BC的长分别为3和4,那么点P到矩形的两条对角线AC和BD的距离之和是 . 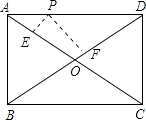
【答案】![]()
【解析】解:过P点作PE⊥AC,PF⊥BD, 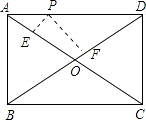
∵四边形ABCD是矩形,
∴AD⊥CD,
∴△PEA∽△CDA,
∴ ![]() ,
,
∵AC=BD= ![]() =5,
=5,
∴ ![]() …①,
…①,
同理:△PFD∽△BAD,
∴ ![]() ,
,
∴ ![]() …②,
…②,
∴①+②得: ![]() ,
,
∴PE+PF= ![]() ,
,
即点P到矩形的两条对角线AC和BD的距离之和是: ![]() .
.
故答案为: ![]() .
.
过P点作PE⊥AC,PF⊥BD,由矩形的性质可证△PEA∽△CDA和△PFD∽△BAD,根据 ![]() 和
和 ![]() ,即
,即 ![]() 和
和 ![]() ,两式相加得PE+PF=
,两式相加得PE+PF= ![]() ,即为点P到矩形的两条对角线AC和BD的距离之和.
,即为点P到矩形的两条对角线AC和BD的距离之和.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目