题目内容
已知a是正整数,若关于x的方程2x-a
-a+4=0至少有一个整数根,则a的值是______.
| 1-x |
2x-a
-a+4=0,
显然满足条件的x,必使得
为整数,否则a=
不可能为整数,
设
=y(y为非负整数),
则原式变为2(1-y2)-ay-a+4=0,
?a=
=2(1-y)+
,
∵y为非负整数 (又1+y能整除4),
∴要使a为整数,则y=0,1,3,
此时a=6,2,-3(不合题意舍去).
故答案为:2或6.
| 1-x |
显然满足条件的x,必使得
| 1-x |
| 2x+4 | ||
|
设
| 1-x |
则原式变为2(1-y2)-ay-a+4=0,
?a=
| 2(1-y2)+4 |
| 1+y |
| 4 |
| 1+y |
∵y为非负整数 (又1+y能整除4),
∴要使a为整数,则y=0,1,3,
此时a=6,2,-3(不合题意舍去).
故答案为:2或6.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 的解是 ( ).
的解是 ( ). ,
,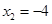
 ,
,