题目内容
若m<n,且|m|>|n|,那么
- A.m一定是正数
- B.m一定是0
- C.m一定是负数
- D.这样的m不存在
C
分析:分m≥0,m<0两种情况讨论,根据绝对值的性质和有理数大小比较的方法求解.
解答:当m≥0时,m<n,且|m|<|n|,不合题意;
当m<0时,n≤0时,|m|>|n|,符合题意;
当m<0时,n>0时,|m|>|n|,符合题意;
当m<0时,n>0时,|m|<|n|,不符合题意.
故若m<n,且|m|>|n|,那么m一定是负数.
故选C.
点评:考查了绝对值的性质,如果用字母a表示有理数,则数a 绝对值要由字母a本身的取值来确定:
①当a是正有理数时,a的绝对值是它本身a;
②当a是负有理数时,a的绝对值是它的相反数-a;
③当a是零时,a的绝对值是零.
分析:分m≥0,m<0两种情况讨论,根据绝对值的性质和有理数大小比较的方法求解.
解答:当m≥0时,m<n,且|m|<|n|,不合题意;
当m<0时,n≤0时,|m|>|n|,符合题意;
当m<0时,n>0时,|m|>|n|,符合题意;
当m<0时,n>0时,|m|<|n|,不符合题意.
故若m<n,且|m|>|n|,那么m一定是负数.
故选C.
点评:考查了绝对值的性质,如果用字母a表示有理数,则数a 绝对值要由字母a本身的取值来确定:
①当a是正有理数时,a的绝对值是它本身a;
②当a是负有理数时,a的绝对值是它的相反数-a;
③当a是零时,a的绝对值是零.

练习册系列答案
相关题目
若a为实数,且a≠0,则下列各式中一定成立的是( )
| A、a2+1>1 | ||
| B、1-a2<0 | ||
C、1+
| ||
D、1-
|
若a+b=-2,且a≥2b,则( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
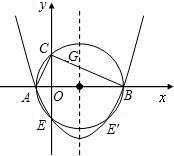 如图,在Rt△ABC中,∠ACB=90°,BC>AC,以斜边AB所在直线为x轴,以斜边AB上的高所在直线为y轴,建立直角坐标系,若OA2+OB2=17,且线段OA、OB的长度是关于x的一元二次方程x2-mx+2(m-3)=0的两个根.
如图,在Rt△ABC中,∠ACB=90°,BC>AC,以斜边AB所在直线为x轴,以斜边AB上的高所在直线为y轴,建立直角坐标系,若OA2+OB2=17,且线段OA、OB的长度是关于x的一元二次方程x2-mx+2(m-3)=0的两个根. (2012•泰州模拟)如图,已知反比例函数
(2012•泰州模拟)如图,已知反比例函数