题目内容
已知如图,矩形ABCD的周长为28,AB=6,对角线AC的垂直平分线分别交AD、BC于E、F,连接AF、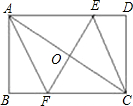 CE、EF,且EF与AC相交于点O.
CE、EF,且EF与AC相交于点O.(1)求AC的长;
(2)求证:四边形AECF是菱形;
(3)求S△ABF与S△AEF的比值.
分析:(1)矩形ABCD的周长为28,AB=6,则可求得BC的值,再根据勾股定理求得AC的值;
(2)要证四边形AFCE是菱形,只需通过定义证明四边相等即可.此题实际是对判定菱形的方法“对角形垂直平分的四边形为菱形”的证明;
(3)因为AE=FC,AO=CO,OE=OF,则可根据SSS证明△AOE≌△COF,所以有S△AEF=S△ACF,再分别求得S△ABF与S△AEF的面积即可得到其比值.
(2)要证四边形AFCE是菱形,只需通过定义证明四边相等即可.此题实际是对判定菱形的方法“对角形垂直平分的四边形为菱形”的证明;
(3)因为AE=FC,AO=CO,OE=OF,则可根据SSS证明△AOE≌△COF,所以有S△AEF=S△ACF,再分别求得S△ABF与S△AEF的面积即可得到其比值.
解答:解:(1)∵ABCD是矩形
∴AB=DC,AD=BC
∵ABCD的周长为28,AB=6
∴AB+DC+AD+BC=28
∴BC=8
∴AC=
=
=10;
(2)∵四边形ABCD是矩形
∴AD∥BC
∴∠OAE=∠OCF
∵EF垂直平分AC
∴AO=CO,∠AOE=∠COF=90°
∴△AOE≌△COF
∴OE=OF
∴四边形AFEC是平行四边形
又∵EF⊥AC
∴四边形AFEC是菱形;
(3)∵AE=FC,AO=CO,OE=OF
∴△AOE≌△COF
∴S△AEF=S△ACF
∵S△ABF=3BF,S△AEF=3FC
∴S△ABF:S△AEF=BF:FC.
设FC=x,则AF=x,BF=8-x
在Rt△ABF中,由勾股定理
62+(8-x)2=x2
解得x=
∴BF=8-x=
∴S△ABF:S△AEF=BF:FC=7:25
∴AB=DC,AD=BC
∵ABCD的周长为28,AB=6
∴AB+DC+AD+BC=28
∴BC=8
∴AC=
| AB2+BC2 |
| 36+64 |
(2)∵四边形ABCD是矩形
∴AD∥BC
∴∠OAE=∠OCF
∵EF垂直平分AC
∴AO=CO,∠AOE=∠COF=90°
∴△AOE≌△COF
∴OE=OF
∴四边形AFEC是平行四边形
又∵EF⊥AC
∴四边形AFEC是菱形;
(3)∵AE=FC,AO=CO,OE=OF
∴△AOE≌△COF
∴S△AEF=S△ACF
∵S△ABF=3BF,S△AEF=3FC
∴S△ABF:S△AEF=BF:FC.
设FC=x,则AF=x,BF=8-x
在Rt△ABF中,由勾股定理
62+(8-x)2=x2
解得x=
| 25 |
| 4 |
∴BF=8-x=
| 7 |
| 4 |
∴S△ABF:S△AEF=BF:FC=7:25
点评:此题主要考查了矩形的性质、线段的垂直平分线性质、菱形的判定以及勾股定理等知识的综合应用,有利于学生思维能力的训练.

练习册系列答案
相关题目
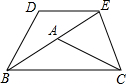 (2012•通州区一模)已知如图,在△ABC中,AB=AC,∠ABC=α,将△ABC以点B为中心,沿逆时针方向旋转α度(0°<α<90°),得到△BDE,点B、A、E恰好在同一条直线上,连接CE.
(2012•通州区一模)已知如图,在△ABC中,AB=AC,∠ABC=α,将△ABC以点B为中心,沿逆时针方向旋转α度(0°<α<90°),得到△BDE,点B、A、E恰好在同一条直线上,连接CE.
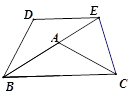
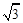 ,请你求出四边形DBCE的面积.
,请你求出四边形DBCE的面积.
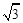 ,请你求出四边形DBCE的面积.
,请你求出四边形DBCE的面积. 已知如图,在△ABC中,AB=AC,∠ABC=α,将△ABC以点B为中心,沿逆时针方向旋转α度(0°<α<90°),得到△BDE,点B、A、E恰好在同一条直线上,连接CE.
已知如图,在△ABC中,AB=AC,∠ABC=α,将△ABC以点B为中心,沿逆时针方向旋转α度(0°<α<90°),得到△BDE,点B、A、E恰好在同一条直线上,连接CE. ,请你求出四边形DBCE的面积.
,请你求出四边形DBCE的面积.