题目内容
【题目】点P到∠AOB的距离定义如下:点Q为∠AOB的两边上的动点,当PQ最小时,我们称此时PQ的长度为点P到∠AOB的距离,记为d(P,∠AOB).特别的,当点P在∠AOB的边上时,d(P,∠AOB)=0.在平面直角坐标系xOy中,A(4,0). 
(1)如图1,若M(0,2),N(﹣1,0),则d(M,∠AOB)= , d(N,∠AOB)=;
(2)在正方形OABC中,点B(4,4).如图2,若点P在直线y=3x+4上,且d(P,∠AOB)=2 ![]() ,求点P的坐标;
,求点P的坐标;
(3)如图3,若点P在抛物线y=x2﹣4上,满足d(P,∠AOB)=2 ![]() 的点P有个,请你画出示意图,并标出点P.
的点P有个,请你画出示意图,并标出点P.
【答案】
(1)1;1
(2)解:如图,当点P在 ![]() 上时,OP=2
上时,OP=2 ![]() ,
,
设P(x,3x+4),则
x2+(3x+4)2=8,
解得 ![]() (舍),
(舍),
∴P(﹣2,﹣2);
点P在射线FG上时,P到射线OB的距离为2 ![]() ,
,
∵点C到OB的距离为2 ![]() ,
,
∴点P与点C重合,
∴P(0,4),
综上所述,P(﹣2,﹣2)或(0,4).
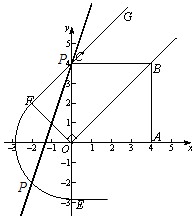
(3)4
【解析】解:(1)∵M(0,2),∠AOB=60°, ∴d(M,∠AOB)= ![]() OM=1;
OM=1;
∵N(﹣1,0),
∴d(N,∠AOB)=ON=1;
所以答案是:1;1.
3)如图所示,点P有4个.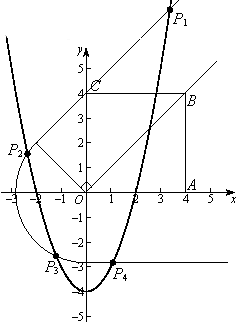
【考点精析】通过灵活运用等腰直角三角形和点到直线的距离,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;从直线外一点到这条直线的垂线段的长度叫做点到直线的距离即可以解答此题.

【题目】表是二次函数y=ax2+bx+c的部分x,y的对应值:
x | … | ﹣1 | ﹣ | 0 |
| 1 |
| 2 |
| 3 | … |
y | … | m |
| ﹣1 |
| ﹣2 |
| ﹣1 |
| 2 | … |
(1)二次函数图象的开口向 , 顶点坐标是 , m的值为;
(2)当x>0时,y的取值范围是;
(3)当抛物线y=ax2+bx+c的顶点在直线y=x+n的下方时,n的取值范围是 .








